直角三角形の三角比（三角比の相互関係、余角の三角比 (\(90°-\theta\))）

今回は、直角三角形の三角比として、三角比の相互関係、余角の三角比 (\(90°-\theta\)) を解説します。

三角比は「三平方の定理」がベースとなっており、その相互関係や余角について考える場合にも、直角三角形をイメージすることが重要になってきます。分からなくなったら、頭の中で直角三角形を思い浮かべてみましょう。

また、「直角三角形の三角比」の学習が終わると、次は「鈍角三角形の三角比」や「三角関数（数学II）」を考えていくことになります。
これらの学習には、当然、「直角三角形の三角比」の知識・理解が前提となってきますので、ぜひこのタイミングで、しっかりと理解を深めるようにしてみてください！

それでは始めていきましょう

解説

三角比の相互関係

\(\sin^{2}\theta+\cos^{2}\theta=1，\tan\theta=\frac{\sin\theta}{\cos\theta}\)

まずは、こちらの等式を考えてみましょう。以下の直角三角形をご覧ください。

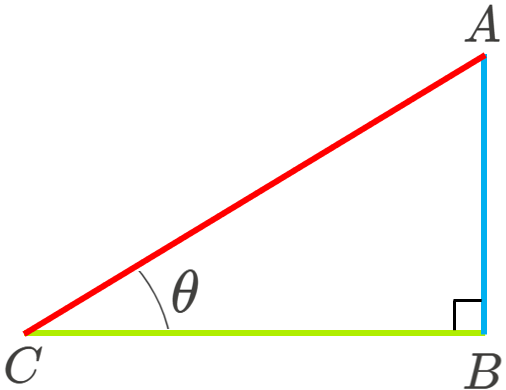
このとき、\(\sin\theta，\cos\theta，\tan\theta\) は、各々以下のように定義されます。

そして、\({①}^{2}+{②}^{2}\) より、

\[\begin{alignat*}{3}
\sin^{2}\theta+\cos^{2}\theta&={\biggl(\frac{\textcolor{#00B0F0}{AB}}{\textcolor{#FF0000}{AC}}\biggr)}^{2}+{\biggl(\frac{\textcolor{#B0EE00}{BC}}{\textcolor{#FF0000}{AC}}\biggr)}^{2} \\
&=\frac{{\textcolor{#00B0F0}{AB}}^{2}+{\textcolor{#B0EE00}{BC}}^{2}}{{\textcolor{#FF0000}{AC}}^{2}}\quad・・・④
\end{alignat*}\]

ここで、\(\triangle ABC\) は、\(\angle ABC=90°\) の直角三角形なので、三平方の定理より、\({\textcolor{#00B0F0}{AB}}^{2}+{\textcolor{#B0EE00}{BC}}^{2}={\textcolor{#FF0000}{AC}}^{2}\)

これを④に代入すると、

\[\begin{alignat*}{3}
\sin^{2}\theta+\cos^{2}\theta&=\frac{{\textcolor{#00B0F0}{AB}}^{2}+{\textcolor{#B0EE00}{BC}}^{2}}{{\textcolor{#FF0000}{AC}}^{2}} \\
&=\frac{{\textcolor{#FF0000}{AC}}^{2}}{{\textcolor{#FF0000}{AC}}^{2}}=1
\end{alignat*}\]

となり、\(\sin^{2}\theta+\cos^{2}\theta=1\) が得られました。

次に、\(\tan\theta=\frac{\sin\theta}{\cos\theta}\) を考えます。

\(\cos\theta=\frac{\textcolor{#B0EE00}{BC}}{\textcolor{#FF0000}{AC}}\) の分子（・分母）は、辺の長さであり、\(\cos\theta=\frac{\textcolor{#B0EE00}{BC}}{\textcolor{#FF0000}{AC}}\ne 0\) です。これに注意して \(\frac{\sin\theta}{\cos\theta}\) を計算すると、

\[\begin{alignat*}{3}
\frac{\sin\theta}{\cos\theta}&=\frac{\bigl(\frac{\textcolor{#00B0F0}{AB}}{\textcolor{#FF0000}{AC}}\bigr)}{\bigl(\frac{\textcolor{#B0EE00}{BC}}{\textcolor{#FF0000}{AC}}\bigr)} \\
&=\frac{\bigl(\frac{\textcolor{#00B0F0}{AB}}{\textcolor{#FF0000}{AC}}\bigr)\times\textcolor{#FF0000}{AC}}{\bigl(\frac{\textcolor{#B0EE00}{BC}}{\textcolor{#FF0000}{AC}}\bigr)\times\textcolor{#FF0000}{AC}} \\
&=\frac{\textcolor{#00B0F0}{AB}}{\textcolor{#B0EE00}{BC}} =\tan\theta\quad (\because\ \tan\theta\ の定義(③))
\end{alignat*}\]

となり、\(\tan\theta=\frac{\sin\theta}{\cos\theta}\) が得られました。

\(1+\tan^{2}\theta=\frac{1}{\cos^{2}\theta}，1+\frac{1}{\tan^{2}\theta}=\frac{1}{\sin^{2}\theta}\)

次に、この2つの等式を見てきます。これらは、先ほど確認した \(\sin^{2}\theta+\cos^{2}\theta=1，\tan\theta=\frac{\sin\theta}{\cos\theta}\) を利用して導出していきます。

ここでも、\(\cos\theta=\frac{\textcolor{#B0EE00}{BC}}{\textcolor{#FF0000}{AC}}\ne 0\ (\because 辺の長さの比)\) であることに注意して、\(\sin^{2}\theta+\cos^{2}\theta=1\) の両辺を、\(\cos^{2}\theta\ (\ne 0)\) で割ると、

\[\begin{alignat*}{3}
&\frac{\cos^{2}\theta+\sin^{2}\theta}{\cos^{2}\theta}=\frac{1}{\cos^{2}\theta} \\
\Leftrightarrow\ &1+\Bigl(\frac{\sin\theta}{\cos\theta}\Bigr)^{2}=\frac{1}{\cos^{2}\theta} \\
\Leftrightarrow\ &1+\tan^{2}\theta=\frac{1}{\cos^{2}\theta}\quad \Bigl(\because\ \tan\theta=\frac{\sin\theta}{\cos\theta}\Bigr)
\end{alignat*}\]

同様に、\(\sin\theta=\frac{\textcolor{#00B0F0}{AB}}{\textcolor{#FF0000}{AC}}\ne 0\ (\because 辺の長さの比)\) であることに注意して、\(\sin^{2}\theta+\cos^{2}\theta=1\) の両辺を、\(\sin^{2}\theta\ (\ne 0)\) で割ると、

\[\begin{alignat*}{3}
&\frac{\sin^{2}\theta+\cos^{2}\theta}{\sin^{2}\theta}=\frac{1}{\sin^{2}\theta} \\
\Leftrightarrow\ &1+\frac{\cos^{2}\theta}{\sin^{2}\theta}=\frac{1}{\sin^{2}\theta} \\
\Leftrightarrow\ &1+\frac{\cos^{2}\theta\times\frac{1}{\cos^{2}\theta}}{\sin^{2}\theta\times\frac{1}{\cos^{2}\theta}}=\frac{1}{\sin^{2}\theta} \\
\Leftrightarrow\ &1+\frac{1}{{\bigl(\frac{\sin\theta}{\cos\theta}\bigr)}^{2}}=\frac{1}{\sin^{2}\theta} \\
\Leftrightarrow\ &1+\frac{1}{\tan^{2}\theta}=\frac{1}{\sin^{2}\theta}\quad \Bigl(\because\ \tan\theta=\frac{\sin\theta}{\cos\theta}\Bigr)
\end{alignat*}\]

となり、\(1+\tan^{2}\theta=\frac{1}{\cos^{2}\theta}，1+\frac{1}{\tan^{2}\theta}=\frac{1}{\sin^{2}\theta}\) の各関係が得られました。

余角の三角比 (\(90°-\theta\))

続いて、角度が \(90°-\theta\) の角の三角比を考えていきます。（このような角を、「余角」といいます）
先ほど見た直角三角形を、改めてご覧ください。

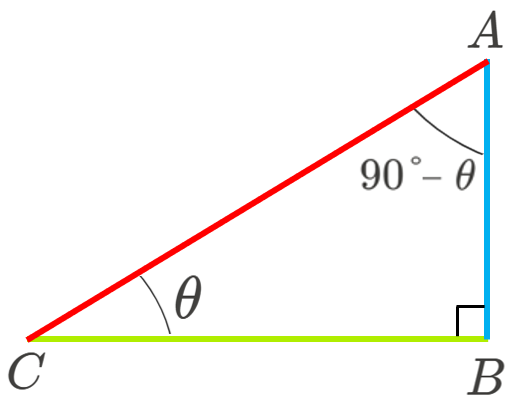
\(\triangle ABC\) は \(\angle ABC=90°\) の直角三角形なので、\(\angle ACB=\theta\) のとき、\(\angle CAB=90°-\theta\) となります。

したがって、

\[\begin{alignat*}{3}
\sin(90°-\theta)&=\sin\angle CAB \\
&=\frac{\textcolor{#B0EE00}{BC}}{\textcolor{#FF0000}{AC}}\quad(\because\ \angle CAB\ についての\ \sin\ の定義)
\end{alignat*}\]

ここで、\(\theta\) に対する、\(\sin，\cos，\tan\) の定義を改めて振り返ると、以下のように定義されるのでした。

これを見ると、\(\sin(90°-\theta)=\frac{\textcolor{#B0EE00}{BC}}{\textcolor{#FF0000}{AC}}\) は、まさに \(\cos\theta\) の定義(②)と一致していることがわかります。

したがって、\(\sin(90°-\theta)=\cos\theta\) が導けました。

同様に、\(\cos(90°-\theta)，\tan(90°-\theta)\) を考えると、

\[\begin{alignat*}{3}
\cos(90°-\theta)&=\cos\angle CAB \\
&=\frac{\textcolor{#00B0F0}{AB}}{\textcolor{#FF0000}{AC}}\quad(\because\ \angle CAB\ についての\ \cos\ の定義) \\
&=\sin\theta\quad(\because\ \sin\theta\ の定義(①))
\end{alignat*}\]

\[\begin{alignat*}{3}
\tan(90°-\theta)&=\tan\angle CAB \\
&=\frac{\textcolor{#B0EE00}{BC}}{\textcolor{#00B0F0}{AB}}\quad(\because\ \angle CAB\ についての\ \tan\ の定義) \\
&=\frac{\textcolor{#B0EE00}{BC}\times\frac{1}{\textcolor{#B0EE00}{BC}}}{\textcolor{#00B0F0}{AB}\times\frac{1}{\textcolor{#B0EE00}{BC}}} \\
&=\frac{1}{\bigl(\frac{\textcolor{#00B0F0}{AB}}{\textcolor{#B0EE00}{BC}}\bigr)} \\
&=\frac{1}{\tan\theta}\quad(\because\ \tan\theta\ の定義(③))
\end{alignat*}\]

となり、\(\cos(90°-\theta)=\sin\theta，\tan(90°-\theta)=\frac{1}{\tan\theta}\) も導くことができました。

なお、\(\tan(90°-\theta)=\frac{1}{\tan\theta}\) は、\(\tan\theta=\frac{\sin\theta}{\cos\theta}\) を利用して導くこともできます。（（※）の式変形で利用しています）

\[\begin{alignat*}{3}
\tan(90°-\theta)&\stackrel{\mathrm{(※)}}{=}\frac{\sin(90°-\theta)}{\cos(90°-\theta)} \\
&=\frac{\cos\theta}{\sin\theta}\ {\small(\because\ \sin(90°-\theta)，\cos(90°-\theta)\ の計算結果)} \\
&=\frac{\cos\theta\times\frac{1}{\cos\theta}}{\sin\theta\times\frac{1}{\cos\theta}} \\
&=\frac{1}{\bigl(\frac{\sin\theta}{\cos\theta}\bigr)} \\
&\stackrel{\mathrm{(※)}}{=}\frac{1}{\tan\theta}
\end{alignat*}\]

（補足）\(\sin，\cos，\tan\) の定義の覚え方

ここまでで、「三角比の相互関係」と「余角の三角比」を見てきたのですが、「そもそも、\(\sin\) は「対辺」だっけ？「隣辺」だっけ・・・？」のような感じで、\(\sin，\cos，\tan\) の定義が覚えにくくて困っている！、という方もいらっしゃるのではないでしょうか。

そんなときに便利なのが、「筆記体の書き方に合わせて覚える」という方法です。

こちらの方法は、非常にシンプルですが、結構使えるイイやつです。ぜひお試しください！

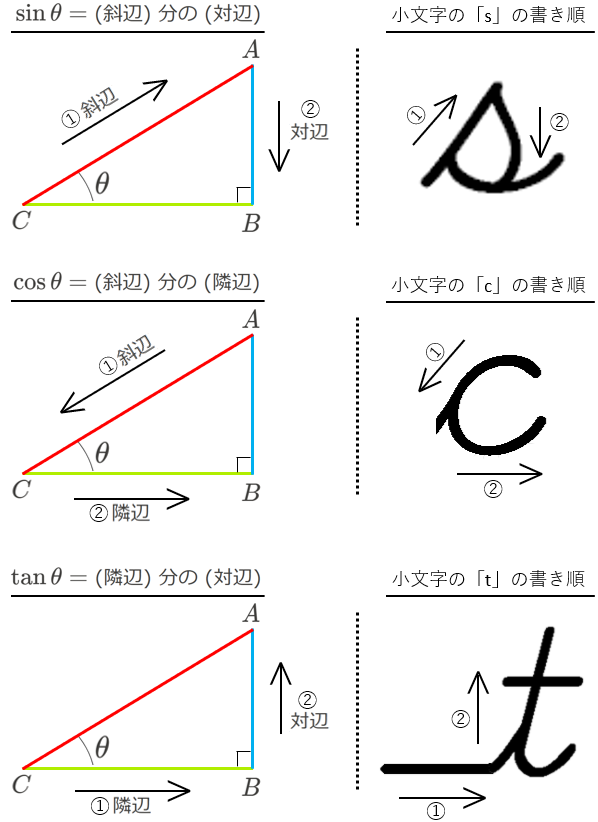
ちなみに、少し学習が進んでいる方だと、「鈍角三角形の三角比」や「三角関数」の勉強をするときに、「座標平面上の単位円で考える」という方法が出てきたと思います。

こちらの方法では、以下のように考えるのでした。

• \(\sin\ \longrightarrow\ y\) 座標
• \(\cos\ \longrightarrow\ x\) 座標
• \(\tan\ \longrightarrow\) 直線の傾き ／ 直線と \(x=1\) との交点の \(y\) 座標

筆記体を思い浮かべるよりも、座標平面上の単位円を考えたほうがわかりやすい、という方は、ぜひこちらの方法を利用するようにしましょう！

※「鈍角三角形の三角比」や「三角関数」についての詳しい解説は、以下のページをご覧ください

おわりに

今回は、直角三角形の三角比（三角比の相互関係、余角の三角比 (\(90°-\theta\))）を解説しました。

各解説を見ると、頭の中に直角三角形を思い浮かべれば、それほど難しいことはやっていないと思っていただけたのではないでしょうか。

今回解説した公式は、どれも非常に重要で、必ず覚えておく必要があるものばかりです。
ぜひ、導出の過程を理解することで、本当に使える公式の習得を目指しましょう！