【三角比の \(\theta\geqq90°\) への拡張】
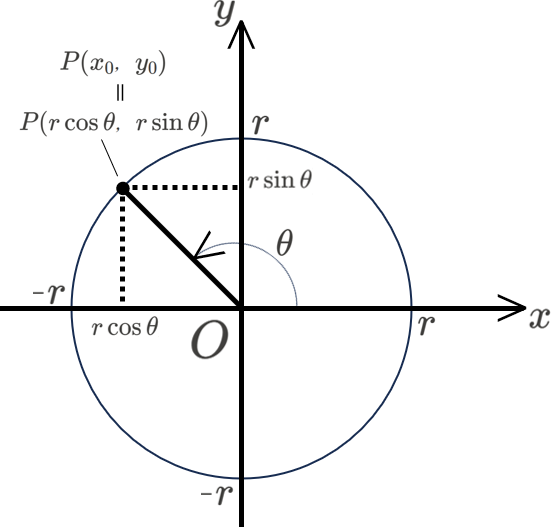
\(xy\) 座標平面に、中心が原点 \(O\)、半径 \(r\) の円をとり、この円周上の点を点 \(P({x}_{0},{y}_{0})\) とする。線分 \(PO\) と\(x\) 軸正の方向とのなす角を \(\theta\) とするとき、\(\sin\theta,\cos\theta,\tan\theta\) を、以下のように定義する。
\[\sin\theta=\frac{{y}_{0}}{r},\cos\theta=\frac{{x}_{0}}{r},\tan\theta=\frac{{y}_{0}}{{x}_{0}}\]
※特に、半径 \(1\) の円(単位円)の場合、
\[\sin\theta={y}_{0},\cos\theta={x}_{0},\tan\theta=\frac{{y}_{0}}{{x}_{0}}\]
解説
\(\theta\geqq90°\) への、三角比の拡張
古代エジプトでは、直角三角形の三角比(相似)を使って、ピラミッドの高さを計測していました。この方法により、人間の身長の何倍もあるピラミッドでも、おおよその高さを知ることができたのです。
現代でも、ビルの高さや山の標高を調べるときは、同様の方法が利用されており、これだけなら、\(0°\)~\(90°\) の範囲の三角比がわかれば、十分に事足ります。
しかし、例えば、超巨大三角チョコパイを作りたい!と思ったとき(そんなことあるかはわかりませんが。。。)、各辺の長さがどのくらいになりそうか調べないと、保管場所を探すことができません。
そして、本家の三角チョコパイを見てみると、どうやら鈍角三角形の形をしていそうです。
こんなとき、まさか、無計画に作った後で保管場所を探すわけにもいかず、鈍角に対する三角比が必要となります。
つまり、実際に超巨大三角チョコパイを作らなくても、鈍角に対する三角比を利用することで、各辺のおおよその長さを予測できるのです。
そして実は、、、この「三角比を \(90°\) 以上に拡張する」という考え方が、メチャクチャ有用なものでした。大学で理工系の分野に進むと、どんな研究をしていても、\(90°\) 以上の角度を入れたものがバンバン出てくることになります。
(※)厳密には「三角関数」という名前になり、慣れ親しんだ「度数法(ex. 30°、60°、、、)」から、「弧度法(ex. \(\frac{\pi}{6}\)、\(\frac{\pi}{3}\)、、、)」へと代入するものが変わります。数学IIで詳しく勉強します。)
これを学べば、\(\sin 120°\) や、\(\cos 150°\) など、直角三角形では考えることのできなかった角度に対しても、三角比を検討できるようになります。
そしてさらにうれしいのは、直角三角形において三角比で学んだ、\(\sin^{2}\theta+\cos^{2}\theta=1\) などの基本的な性質や、鈍角三角形に対する正弦定理や余弦定理までも考えることができます。
それでは早速、三角比の \(\theta\geqq90°\) への拡張を見ていきましょう!
直角三角形で得られた性質から、三角比を再定義する
以下のように、\(xy\) 平面上に、中心が原点 \(O\)、半径 \(r\) の円をとります。そして、この座標平面の第1象限(\(x\) が正、\(y\) が正の範囲)にある円 \(O\) の円周上の任意の点を \(P({x}_{0},{y}_{0})\)とします。また、点 \(P\) から \(x\) 軸に下ろした垂線の足を \(H\) と定めます。
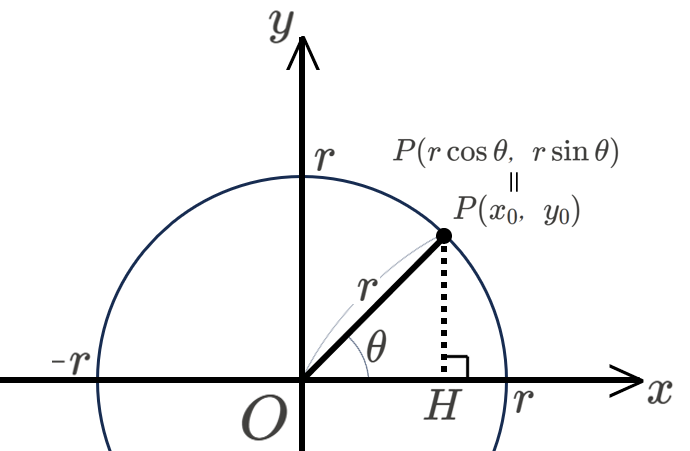
このとき、線分 \(PO\) と\(x\) 軸正の方向とのなす角を \(\theta\) とすると、\(\sin\theta,\cos\theta,\tan\theta\) は、直角三角形における三角比の定義から、以下のように表すことができます。
\[\begin{alignat*}{3}
&\sin\theta=\frac{PH}{OP},\cos\theta=\frac{OH}{OP},\tan\theta=\frac{PH}{OH} \\
\Leftrightarrow\ &\sin\theta=\frac{{y}_{0}}{r},\cos\theta=\frac{{x}_{0}}{r},\tan\theta=\frac{{y}_{0}}{{x}_{0}}
\end{alignat*}\]
これは、座標平面上に点 \(P\),\(H\) をとり、直角三角形の三角比の定義を適用した結果、たまたま得られた関係です。
直角三角形以外に拡張するにあたり、この関係(性質)を利用します。
つまり、直角三角形でたまたま得られた性質を、それ自体、三角比の定義として再定義してしまうのです。
具体的には、三角比を、以下のように定義します。
【三角比の \(\theta\geqq90°\) への拡張】
\(xy\) 座標平面に、中心が原点 \(O\)、半径 \(r\) の円をとり、この円周上の点を点 \(P({x}_{0},{y}_{0})\) とする。線分 \(PO\) と\(x\) 軸正の方向とのなす角を \(\theta\) とするとき、\(\sin\theta,\cos\theta,\tan\theta\) を、以下のように定義する。
\[\sin\theta=\frac{{y}_{0}}{r},\cos\theta=\frac{{x}_{0}}{r},\tan\theta=\frac{{y}_{0}}{{x}_{0}}\]
このように再定義すれば、座標平面なので、例えば、点 \(P\) を第2象限(\(x\) が負、\(y\) が正の範囲)にとることもでき、\(\theta\) が鈍角の場合もカバーできます。(超巨大三角チョコパイもOK!)
なお、第2象限にとった場合、\({x}_{0}\) は負の数なので、\(\cos\theta=\frac{{x}_{0}}{r},\tan\theta=\frac{{y}_{0}}{{x}_{0}}\) は負の数になることに注意してください。(第2象限でも、\({y}_{0}\) は正の数なので、\(\sin\theta=\frac{{y}_{0}}{r}\) は正の数となります。)
具体例
それでは、少し具体例を見てみましょう。
【\(120°\)】
座標平面上の円周上の点 \(P\) を、次の図のように、線分 \(PO\) と\(x\) 軸正の方向とのなす角が \(120°\) となるようにとります。
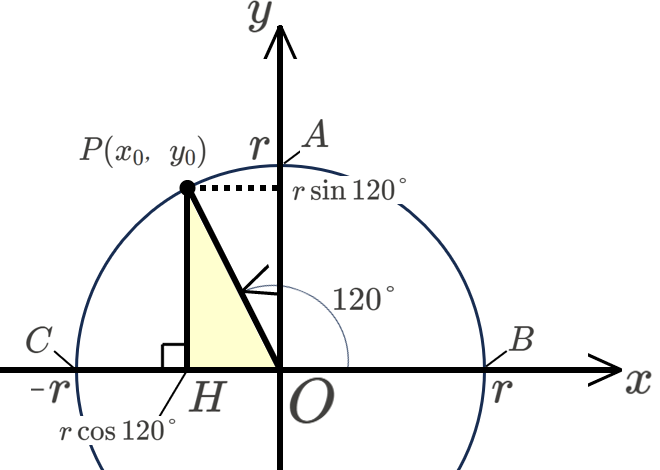
まず、\(\triangle OPH\) について、直角三角形の三角比を利用して、点 \(P\) の座標を具体的に計算してみましょう。
\(\angle POA=\angle POB-\angle AOB\) で、\(\angle POB=120°,\angle AOB=90°\) なので、\(\angle POA=120°-90°=30°\) です。
そして、\(\angle AOC=90°\) なので、
\[\begin{alignat*}{3}
\angle POH&=\angle AOC-\angle POA \\
&=90°-30°=60°
\end{alignat*}\]
これを利用して、直角三角形 \(OPH\) の \(\angle POH\) に対する三角比を考えると、
\(\sin\angle POH=\frac{PH}{OP},\cos\angle POH=\frac{OH}{OP}\)
\[\Leftrightarrow\ PH=OP\sin 60°,OH=OP\cos 60°\]
\[\therefore\ PH=\frac{\sqrt{3}}{2}r,OH=\frac{1}{2}r\]
したがって、点 \(P\) の \(x\) 座標は負であることに注意すると、点 \(P\) の座標は、\(P(-\frac{1}{2}r,\frac{\sqrt{3}}{2}r)\) とわかります。
一方で、\(\sin 120°,\cos 120°,\tan 120°\) は、先ほど見た円周上の点を利用した定義から、点 \(P\) の座標 \(P({x}_{0},{y}_{0})\) を用いて、以下の通り表せます。
\[{\small\sin 120°=\frac{{y}_{0}}{r},\cos 120°=\frac{{x}_{0}}{r},\tan 120°=\frac{{y}_{0}}{{x}_{0}}}\]
点 \(P\) の座標 \(P({x}_{0},{y}_{0})\) は、\((-\frac{1}{2}r,\frac{\sqrt{3}}{2}r)\) なので、これを代入して、
\[\sin 120°=\frac{\frac{\sqrt{3}}{2}r}{r}=\frac{\frac{\sqrt{3}}{2}r\times\frac{2}{r}}{r\times\frac{2}{r}}=\frac{\sqrt{3}}{2}\]
\[\cos 120°=\frac{-\frac{1}{2}r}{r}=-\frac{\frac{1}{2}r\times\frac{2}{r}}{r\times\frac{2}{r}}=-\frac{1}{2}\]
\[\tan 120°=\frac{\frac{\sqrt{3}}{2}r}{-\frac{1}{2}r}=-\frac{\frac{\sqrt{3}}{2}r\times\frac{2}{r}}{\frac{1}{2}r\times\frac{2}{r}}=-\sqrt{3}\]
となり、\(\sin 120°,\cos 120°,\tan 120°\) の各値が得られました!
【\(225°\)】
先ほどの \(120°\) の場合と同様に、
- 座標平面上の円 \(O\)
- その円周上にあり、線分 \(PO\) と\(x\) 軸正の方向とのなす角が \(225°\) となるような点 \(P\)
- 点 \(P\) から \(x\) 軸に下した垂線の足 \(H\)
をとると、以下の図のようになります。
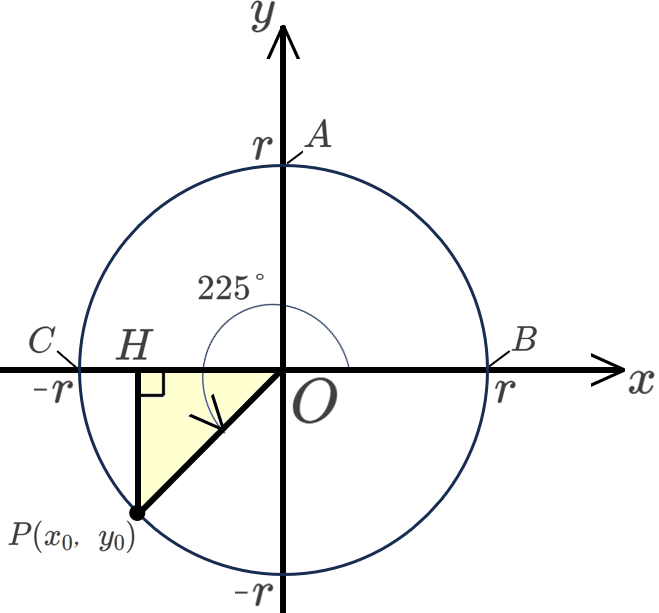
\(\angle POH=45°\ (\ =225°-180°)\) なので、
\[PH=OP\sin\angle POH=r\sin 45°=\frac{r}{\sqrt{2}}\]
\[OH=OP\cos\angle POH=r\cos 45°=\frac{r}{\sqrt{2}}\]
となり、点 \(P\) の \(x\) 座標、\(y\) 座標がともに負であることに注意すると、点 \(P\) の座標は、\(P(-\frac{r}{\sqrt{2}},-\frac{r}{\sqrt{2}})\) とわかりました。
したがって、円周上の点を利用した定義を利用して、\(\sin 225°,\cos 225°,\tan 225°\) を計算すると、
\[\sin 225°=\frac{-\frac{r}{\sqrt{2}}}{r}=-\frac{1}{\sqrt{2}}\]
\[\cos 225°=\frac{-\frac{r}{\sqrt{2}}}{r}=-\frac{1}{\sqrt{2}}\]
\[\tan 225°=\frac{-\frac{r}{\sqrt{2}}}{-\frac{r}{\sqrt{2}}}=1\]
となり、\(\sin 225°,\cos 225°,\tan 225°\) の各値が得られました!
重要な5つの補足
(補足①)座標平面で再定義すれば、三角形じゃなくても三角比を考えられる
今までで、\(225°\) の場合の \(\sin,\cos,\tan\) を検討してきましたが、「あれ?」と思われた方もいらっしゃるかもしれません。
そうです。三角形の内角の和は \(180°\) なので、1つの角が \(225°\) では三角形になりません。
実は、この点が非常にありがたいポイントです。
というのも、元々、鈍角三角形の三角比を考えたい!というモチベーションで、三角比の拡張を考えてきたのですが、座標平面で三角比を再定義することで、三角形にすら限定する必要がなくなりました。
この結論を利用すれば、\(360°\) を超える角に対しても、三角比(三角関数)を考えることが可能です!
(補足②)拡張後の定義でも、基本公式や、正弦定理・余弦定理が成立する
上記のように、【三角比を座標平面で再定義する】というのは、非常に優れたアイデアだったということがわかりました。
、、、しかし、ちょっと待ってください。
直角三角形の三角比を考えたときは、以下の等式が成り立つのでした。
【三角比の相互関係】
\(0°<\theta<90°\) を満たす \(\theta\) に対して、
\[\sin^{2}\theta+\cos^{2}\theta=1\]
\[\tan\theta=\frac{\sin\theta}{\cos\theta}\]
\[1+\tan^{2}\theta=\frac{1}{\cos^{2}\theta}\]
\[1+\frac{1}{\tan^{2}\theta}=\frac{1}{\sin^{2}\theta}\]
また、これに加えて、鋭角三角形の辺と角の関係として、正弦定理や余弦定理という重要な定理がありました。
再定義した三角比でも、これらの性質・定理は成立してほしいですよね?
(というよりも、直角三角形までで得られたこれらの性質が失われているとすると、【三角比を座標平面で再定義する】というアイデアは、表面上は使えそうでも、実際はダメダメだった、ということになるかもしれません)
そこで、実際に検討してみると、これらは拡張後の定義でも成立することがわかります!
今回は、解説が非常に長くなってしまうため割愛しましたが、【三角比の相互関係】については、座標平面で再定義した \(\sin\theta,\cos\theta,\tan\theta\) を、それぞれの相互関係の式に代入すれば、すぐに成立することが確かめられます。
また、【正弦定理・余弦定理】については、こちらのページで、鈍角三角形も想定した導出を行っていますので、是非一読ください。
(補足③)半径が \(1\)(単位円)の場合、\(\sin,\cos\) は「単位円の座標」になる
今まで、こちらの定義で、\(\theta\geqq 90°\) の場合の三角比を考えてきたのですが、
\[\sin\theta=\frac{{y}_{0}}{r},\cos\theta=\frac{{x}_{0}}{r},\tan\theta=\frac{{y}_{0}}{{x}_{0}}\]
実は、この定義には、少々無駄な文字が混ざっています。。それはズバリ、半径 \(r\) です。
上の具体例で見たように、
\[{\small\sin 120°=\frac{\sqrt{3}}{2},\cos 120°=-\frac{1}{2},\tan 120°=-\sqrt{3}}\]
\[{\small\sin 225°=-\frac{1}{\sqrt{2}},\cos 225°=-\frac{1}{\sqrt{2}},\tan 225°=1}\]
となり、半径 \(r\) によらずに定義できることがわかります。
その理由は、計算してみるとすぐにわかりますが、\({x}_{0},{y}_{0}\) が、「\(r\times○\)」の形で表され、最終的に、\(r\) が分母・分子で約分されてしまうためです。
、、、であれば、初めから \(r\) をなくしてしまってもよいわけで、今後は、半径 \(r=1\) を代入した、以下の式で見ることが増えると思います。(このような半径 \(1\) の円のことを単位円といいます)
\[\sin\theta={y}_{0},\cos\theta={x}_{0},\tan\theta=\frac{{y}_{0}}{{x}_{0}}\]
この表し方をした場合、\(\sin,\cos\) は、「座標平面上における、単位円上の点の座標」と言い換えることができます。
(補足④) \(\tan\) は直線の傾き
三角比を座標平面を利用して再定義したことで、単位円上の点 \(P({x}_{0},{y}_{0})\) の座標を用いて、
\[\tan\theta =\frac{{y}_{0}}{{x}_{0}}\]
とできたのでした。
ここで、この \(\frac{{y}_{0}}{{x}_{0}}\) という形。何か見覚えありませんか?
・・・そうです!直線の傾きを表しています。
【(復習)直線の傾き】
\(l:y=ax+b\) という直線の傾き \(m\) は、以下の式で表される。
\[m=\frac{yの変化量}{xの変化量}\]
したがって、上で見た、単位円における \(\sin,\cos\) と合わせて、以下のように整理できます。
| \(\sin\) | 座標平面上の単位円 \(O\) 上の点\(P\) の \(x\) 座標 |
| \(\cos\) | 座標平面上の単位円 \(O\) 上の点\(P\) の \(y\) 座標 |
| \(\tan\) | 座標平面上の単位円 \(O\) 上に点\(P\) をとった時の直線 \(PO\) の傾き |
(補足⑤)\(0°,90°,180°,270°\) の三角比
前の表で見た通り、\(\sin,\cos\) は「単位円の座標」と考えることができたのでした。
そこで、これを利用して、特別な角として、\(0°,90°,180°,270°\) の三角比を考えてみましょう。
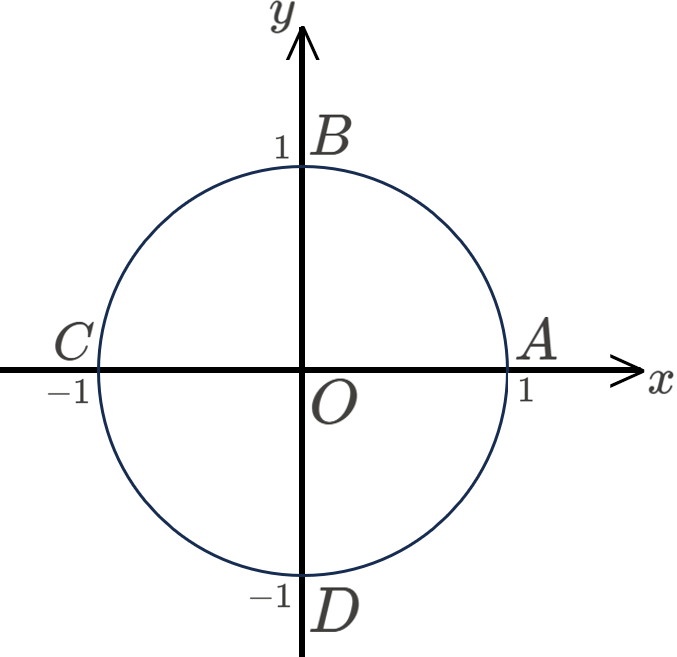
まず、\(0°\) の場合、 \(\sin,\cos\) は点 \(A\) の座標 \((1,0)\) となります。したがって、\((\cos 0°,\sin 0°)=(1,0)\) です。
そして、【三角比の相互関係】から、\(\tan 0°=\frac{\sin 0°}{\cos 0°}=\frac{0}{1}=0\)となります。
同様に、\(180°\) 場合は、点 \(C\) の座標 \((-1,0)\) より、\((\sin 180°,\cos 180°,\tan 180°)=(0,-1,0)\) となります。
次に、\(90°\) の場合ですが、点 \(B\) の座標 \((0,1)\) から、\((\cos 90°,\sin 90°)=(0,1)\) となり、ここまでは全く問題ありません。
続いて、\(\tan\ (=\frac{{y}_{0}}{{x}_{0}})\) を考えたいのですが、点 \(B\) の \(x\) 座標が \(0\) のため定義できません。
同様に、\(270°\) の場合も、\(\tan\) は定義できません。
\(\theta=90°+(180°\times n)\ (n\) は \(0\) 以上の整数\()\) の場合、\(\tan\) は定義できない
これは、特に、\(\tan\) が直線の傾きである、という結果とも整合します。(\(90°\) の場合は、\(x=0\) という特別な形をした直線になります。)
整理すると、角度毎の三角比の値は、以下の通りとなります。
| \(\theta\) | \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
| 0° | 0 | 1 | 0 |
| 90° | 1 | 0 | (定義できない) |
| 180° | 0 | -1 | 0 |
| 270° | -1 | 0 | (定義できない) |
おわりに
お疲れさまでした!今回は、三角比の鈍角への拡張を見てきました。
直角三角形の世界で定義された「三角比」が、直角三角形を超え、一般の角でも考えられると知って、少々混乱されている方もいらっしゃるかもしれません。
今、この瞬間から、みなさんは、三角比は、
- × 直角三角形の角と対応する辺の比
ではなく、 - ○ 座標平面上の単位円上の点の座標
と、意識するようにしてみましょう。
このように、少しだけ見方を変えるだけで、直角三角形という限られた場合だけしか使えない(ショボい)ものから、メチャメチャ有能な使える武器に大変身します!
ぜひ、ほんの少し見方を変えて、有能な武器を使いこなせるようになりましょう!



コメント