三角関数の公式まとめ（マイナスの角・\(\pm\pi/2\)・\(\pm\pi\)）

解説

覚えるのは3つだけ！試験の現場での立ち向かい方

今回は、三角関数の各種公式を解説します。

ただ、三角関数の分野は、公式が多すぎて、覚えきれない・・・　と悩んでいる方も多いのではないでしょうか。
私も、その気持ちは、非常によくわかります（実際、私も、全ては覚えていません。。。）

では、どうやって問題を解いているのか。
中途半端に覚えた状態で公式を使うと、間違った公式を適用して、間違った計算にもなりかねません。

ポイントは、試験の現場で、覚えていない（もしくは、自信のない）変換が必要になったときは、自分で公式を導出するということです。

そこで、今回の解説では、公式の導出自体ではなく、三角関数の変換が必要になったときに、どうやって立ち向かえばよいか、という観点で説明します。

これを身につければ、

• 覚えることが少なくなる（最低限の3つだけ覚えればOK）
• あやふやな知識を適用して間違った計算をするリスクが減る

と、一石二鳥です！それでは早速見ていきましょう。

公式の導出は、以下の 5 Stepで行います。
（Step0は「事前準備」、Step1～4は「試験の現場」での手順です）

【Step 0】　最低限として、以下のABCを丸暗記しておく。

• A.　\(-\theta\)　→　\(\sin\) は 「－」 、\(\cos\) は 「＋」が前に出る
• B.　\(\theta\pm\pi/2\) 　→　\(\sin\) と \(\cos\)が入れ替わる（\(\sin\) は \(\cos\) 、\(\cos\) は \(\sin\)）
• C.　\(\theta\pm\pi\) 　→　そのまま（\(\sin\) は \(\sin\) 、\(\cos\) は \(\cos\)）

これだけは、最低限として、覚えておくようにしましょう。

、、、とはいえ、緊張などでどうしても忘れてしまうこともあると思います。
その場合は、頭に単位円を思い浮かべて、\(\sin\) と \(\cos\) は入れ替わりそうか、そのままっぽいかを、なんとかひねり出しましょう。諦めたらそこで試合終了です。

【Step1】　BCが使える状態にするため、Aを適用する

例えば、\(\sin(\pi/2-\theta)\) を考えます。
このままでは、BCのいずれにも当てはまらないので、BCが使えません。

そこで、BCを使えるように（無理やり）Aを使って変換することを考えます。具体的には、

\[\begin{alignat*}{3}
\sin(\pi/2-\theta)&=\sin\{-(\theta-\pi/2)\}&&(変換①)\\
&=-\sin(\theta-\pi/2)\quad(\because 上のA)&\qquad&(変換②)
\end{alignat*}\]

このとき、とりあえず、Aを使ってみよう！　ではなく、

• BCを使える形を、無理やり、作る（変換①）
• 変換①で不要な（邪魔な）符号が出てきたので、Aを使って調整する（変換②）

という頭の使い方をしている点に注意してください。
この発想がないと、やみくもに変換を繰り返して、試験時間のムダ遣いになりかねません。

【Step2】　とりあえず、BCを適用した結果を計算用紙に書く

Step1で、BCが使えるようになったので、実際にBCを適用します。
このとき、マイナスを付け加えられるように、少しだけ隙間を開けておくのがポイントです。（以下の？の部分）

\[\begin{alignat*}{3}
\sin(\pi/2-\theta)&=-\sin(\theta-\pi/2) \\
&=-(\ ?\ \cos\theta)\quad(\because 上のB)
\end{alignat*}\]

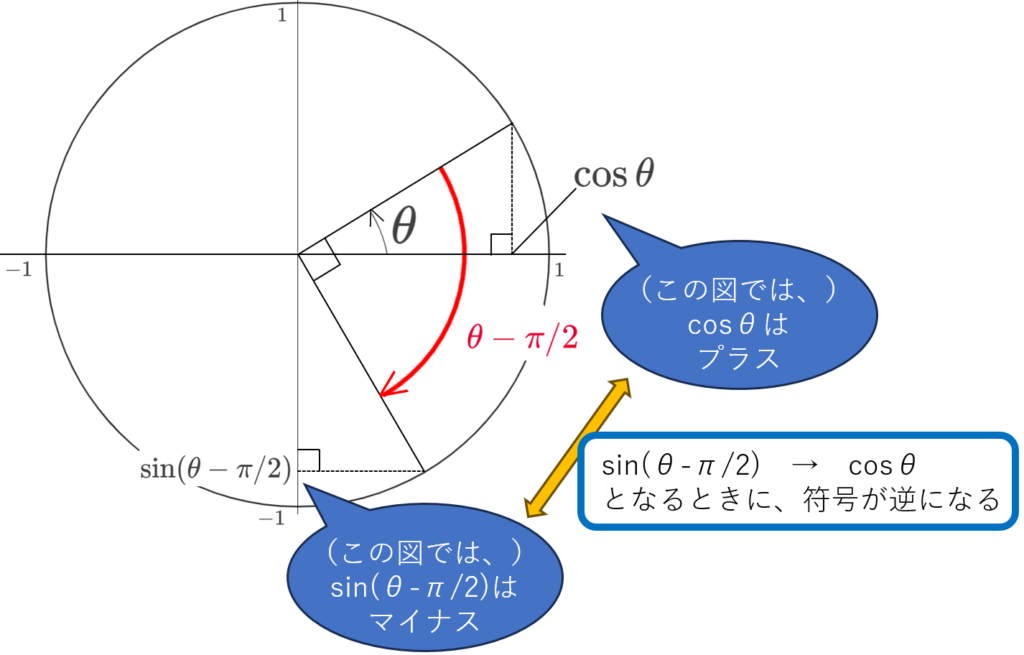
【Step3】　単位円を頭に思い浮かべて、プラスか、マイナスかを決定する

BCを適用する際に、符号が逆になる（変換の時にマイナスがつく）場合があります。
そこで、符号はそのままか、逆になるかを、単位円を思い浮かべて、決定していきます。

なお、ミスをなるべく減らすため、慣れない内は、実際に単位円を描いてみることをおススメします。慣れてくれば、時間節約のため、頭の中でパパっとやってしまいましょう。

\[\begin{alignat*}{3}
\sin(\pi/2-\theta)&=-\sin(\theta-\pi/2) \\
&=-(-\ \cos\theta)\quad(\because 下の図)
\end{alignat*}\]

【Step4】　式をきれいにして計算終了

\[\begin{alignat*}{3}
\sin(\pi/2-\theta)&=-(-\ \cos\theta) \\
&=\cos\theta
\end{alignat*}\]

これで、無事に、使いやすい形に変換できました。

この手順を踏めば、基本的にどのような変換も可能です（少なくとも高校で出てくる範囲では）。

今回は説明のため、5Stepに分けて説明しましたが、慣れてくれば、単位円を頭に思い浮かべるだけで、一気に最終結果を導くこともできるようになると思います。
何度も練習して、ぜひ、こちらの式変形をマスターしてください！

\(\tan\) の式変形

ここまでの解説で、\(\sin\) と \(\cos\) の式変形を見てきました。

、、、と、ここで、「\(\tan\) はどうしたらいいの？」と思われたかもしれません。
実は、\(\tan\) は、\(\sin\) と \(\cos\) の式変形から、簡単に導くことができます。

例として、\(\tan(\pi/2+\theta)\) を考えてみましょう。ポイントは、\(\tan=\frac{\sin}{\cos}\) という関係です。

\[\begin{alignat*}{3}
\tan(\pi/2+\theta)&=\frac{\sin(\pi/2+\theta)}{\cos(\pi/2+\theta)}&\quad&(\because\tan=\frac{\sin}{\cos}) \\
&=\frac{-\cos\theta}{\sin\theta}&&(\because 上のStep0～4) \\
&=-\frac{1}{\frac{\sin\theta}{\cos\theta}} \\
&=-\frac{1}{\tan\theta}&&(\because\tan=\frac{\sin}{\cos})
\end{alignat*}\]

となり、導出できました。

もし、その他のパターンが出題された場合でも、\(\tan=\frac{\sin}{\cos}\) という関係に注意すれば、同様に導出することができます。

おわりに

今回は、三角関数の各種公式について、試験の現場での立ち向かい方を解説しました。

三角関数の攻略のコツは、

• 覚えるのは必要最小限にとどめる
• 試験の現場で、1秒でも早く式変形できるよう、何度も練習する

ということに尽きます。

特に、練習の際は、必ず単位円を描いてみることを強くおススメします。
事前準備として、単位円を描いて公式を導出した経験が、きっと実際の試験で皆さんを助けてくれると思います。

ぜひ、何度も練習を繰り返し、試験の現場で使える力を身につけましょう！