三角形の内角の二等分線と、辺の比

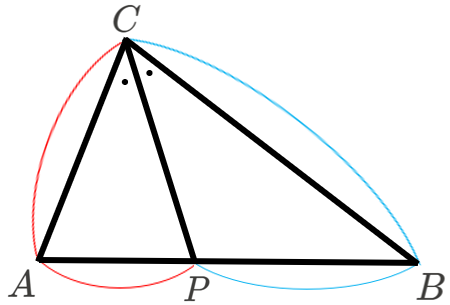
今回は、三角形の内角の二等分線と、辺の比に関する定理を解説します。

こちらの定理は、定理自体の証明というよりも、共通テストの図形問題や、ベクトル（数学III）などで非常によく利用します。

定理を使ったことはあるけど、なぜ成り立つのかは、イマイチよくわからない、という方も結構いらっしゃるかと思います。ぜひ、今回の解説を通して、「なんとなく成立しそう」から卒業して、自信をもって定理を使いこなせるようになりましょう！

ちなみに、似たような定理として、「三角形の外角の二等分線と、辺の比に関する定理」というのも存在します。
こちらは、少々マイナーで、使う機会もそれほど多くはないと思われるため、今回の解説からは外しました。また機会があれば、別のところで解説してみたいと思います。

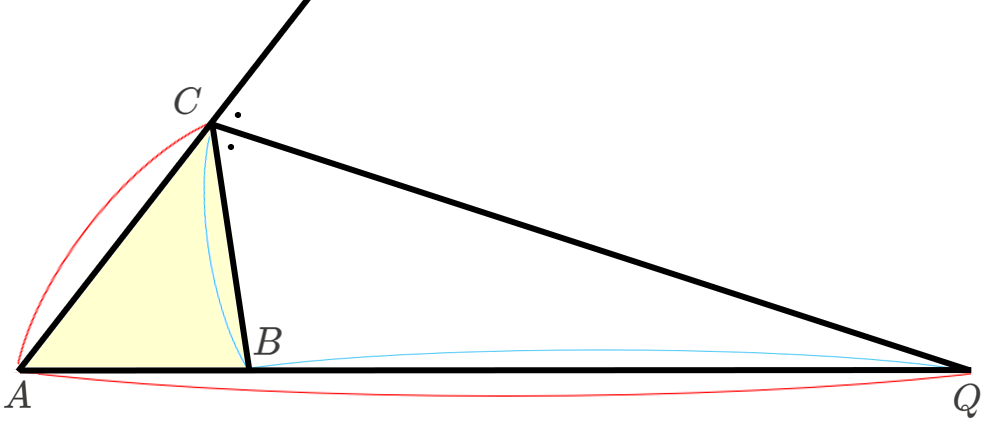
解説

それでは、解説に入ります。以下のような図形を考えてみます。

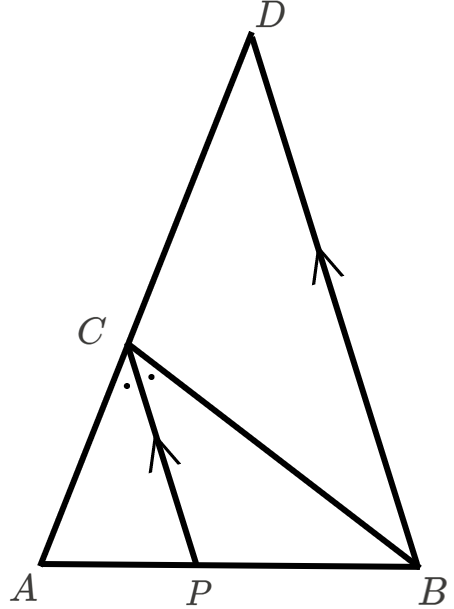
まず、点\(B\) から \(CP\) に平行な直線を引きます。
そして、それと辺 \(AC\) を \(C\) 方向に延長した直線の交点を、点 \(D\) としました。

ここで、\(CP\ /\!/\ DB\) のため、以下の関係にあることがわかります。

• \(\angle PCB=\angle CBD\ (\because\ 錯角)\)
• \(\angle ACP=\angle CDB\ (\because\ 同位角)\)

このことから、\(\angle CBD=\angle CDB\) のため、\(\triangle CBD\) は、\(CB=CD\) の二等辺三角形となります。

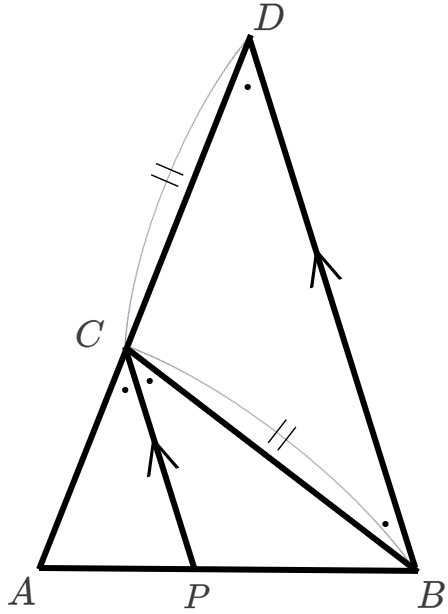
一方で、\(\triangle ACP\) と \(\triangle ADB\) は、

• \(\angle CAP=\angle DAB\ (\because\ 角を共有)\)
• \(\angle ACP=\angle ADB\ (\because\ 同位角)\)

から、\(\triangle ACP\) ∽ \(\triangle ADB\) となります（三角形の2つの角が等しい）。

\(\triangle ACP\) と \(\triangle ADB\) の相似比を考えると、

\[AP:PB=AC:CD\]

であり、上で見た通り、\(\triangle CBD\) は、\(CB=CD\) の二等辺三角形のため、

\(AP\) : \(PB\) \(=\) \(AC\) : \(CD\)
\(\Leftrightarrow\) \(AP\) : \(BP\) \(=\) \(CA\) : \(CB\)

となって、\(AP\) : \(BP\) \(=\) \(CA\) : \(CB\) という関係が得られました。

おわりに

お疲れさまでした！今回は、三角形の内角の二等分線と、辺の比に関する定理を見てきました。

よく使う定理のわりに、証明をした経験がある、という方は、意外と少なかったのではないでしょうか。

証明自体は結構あっさりしていて、一度身に着けてしまえば、自力でも、比較的簡単に証明できます。
ぜひ、「大体どういう流れで証明していた」のか復習し、自信をもって定理を使うことができるようになりましょう！

ちなみに、、、

こちらの定理にも、「方べきの定理」のような、通称？愛称？のようなものがあればいいのですが、
毎回、「三角形の内角の二等分線と、辺の比の定理」のような呼び方をしていて、伝わりづらさにモヤモヤしています。。。

もしご存じの方がいらっしゃったら、コメントで教えていただけるとありがたいです！