【正弦定理】
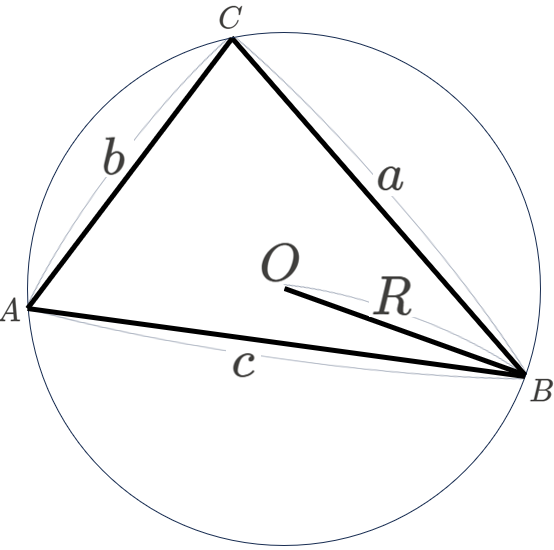
\(\triangle ABC\) の外接円の半径を \(R\) とすると、以下の等式が成り立つ。
\[\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R\]
\[\sin A\ :\ \sin B\ :\ \sin C=a\ :\ b\ :\ c\]
(\(a\),\(b\),\(c\) は各々、角 \(A\),\(B\),\(C\) に向かい合う辺の長さ)
【余弦定理】
\(\triangle ABC\) において、以下の等式が成り立つ。
\({a}^{2}={b}^{2}+{c}^{2}-2bc\cos A\)
\({b}^{2}={c}^{2}+{a}^{2}-2ca\cos B\)
\({c}^{2}={a}^{2}+{b}^{2}-2ab\cos C\)
(\(a\),\(b\),\(c\) は各々、角 \(A\),\(B\),\(C\) に向かい合う辺の長さ)
解説
正弦定理
まずは、正弦定理について見ていきましょう。
証明は、(i) \(0°<C<90°\),(ii) \(C=90°\),(iii) \(90°<C<180°\) の3つの場合に分けて考えます。
なお、ここでは、\(\frac{c}{\sin C}=2R\) が成立することだけ証明します。
(残りの角・辺のペアは、同じ要領で考えれば、\(2R\) となることが確認できます)
(i) \(0°<C<90°\) の場合
\(\triangle ABC\) の外接円 \(O\) の同一円周上に、\(AC’\) が中心 \(O\) を通るように、点 \(C’\) をとります。
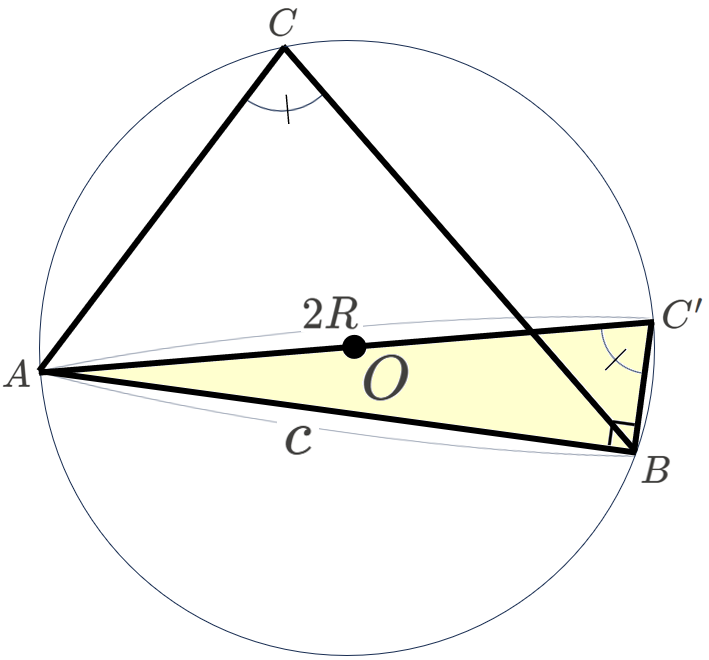
このとき、\(\angle C,\angle C’\) は、いずれも弧 \(\stackrel{\huge\frown}{AB}\) に対する円周角のため、円周角の定理より、\(\angle C=\angle C’\) となり、\(\sin C=\sin C’\) であることがわかります。
一方で、\(\triangle ABC’\) に注目すると、\(\angle B\) は、弧 \(\stackrel{\huge\frown}{AC’}\) に対する円周角であり、\(AC’\) は円 \(O\) の直径のため、円周角の定理より、\(\angle B=90°\) です。
したがって、\(\sin C’\) は、直角三角形 \(ABC’\) に対する \(\sin\) の定義より、\(\sin C’=\frac{AB}{AC’}\)
この式に、\(\sin C’=\sin C,AB=c,AC’=2R\) を代入すると、
\[\sin C=\frac{c}{2R}\]
\(0°<C<90°\) のとき、\(\sin C\ne 0\) であることに注意して、両辺に \(\frac{2R}{\sin C}\) をかけ、左辺と右辺を入れ替えると、
\[\frac{c}{\sin C}=2R\]
となり、求める式が得られました。
(ii) \(C=90°\) の場合
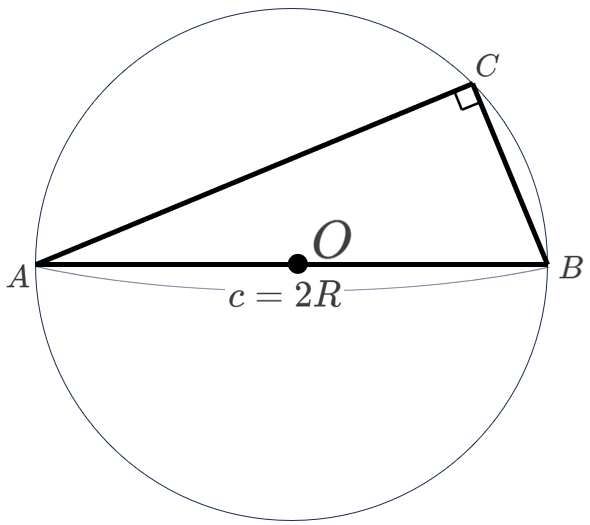
円周角の定理の逆より、\(AB\) は、円 \(O\) の直径です。したがって、\(c=AB=2R\) となります。
一方で、\(\sin C=\sin 90°=1\) なので、
\[\frac{c}{\sin C}=\frac{2R}{1}=2R\]
となり、求める式が得られました。
(iii) \(90°<C<180°\) の場合
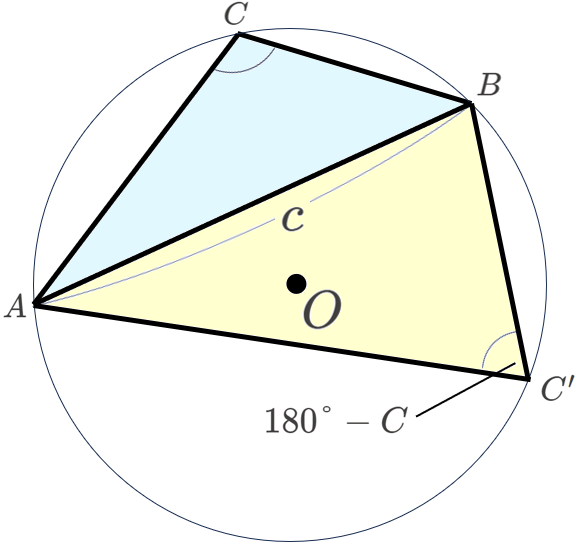
円 \(O\) の弧 \(\stackrel{\huge\frown}{AB}\) に対し、点 \(C\) が存在しない方の弧に点 \(C’\) をとると、円周角の定理より、\(C’=180°- C\) となります。
ここで、今、\(90°<C<180°\) なので、
\[{\small\begin{alignat*}{3}
&90°<C<180° \\
\Leftrightarrow\ &-180°<-C<-90°\ &&(※\ 辺々にマイナスをかける) \\
\Leftrightarrow\ &0°<180°- C<90°&&(※\ 辺々に180°を足す) \\
\Leftrightarrow\ &0°<C'<90°&&(※\ C’=180°- C)
\end{alignat*}}\]
に注意すると、\(\triangle ABC’\) の \(\angle C’\) に、(i) \(0°<C<90°\) の場合の正弦定理を適用して、
\[\frac{AB}{\sin C’}=\frac{c}{\sin C’}=2R\]
そして、\((C’=180°- C)\ \Leftrightarrow\ (C=180°- C’)\) で、\(\sin(180°- C’)=\sin C’\) なので、
\[\begin{alignat*}{3}
\frac{c}{\sin C}&=\frac{c}{\sin(180°- C’)} \\
&=\frac{c}{\sin C’}=2R
\end{alignat*}\]
となり、求める式が得られました。
余弦定理
続いて、余弦定理を見ていきます。
なお、ここでも、\({c}^{2}={a}^{2}+{b}^{2}-2ab\cos C\) が成立することだけ証明します。
(残りの角・辺については、\(x\) 座標、\(y\) 座標の取り方を変えれば、同様に確認できます)
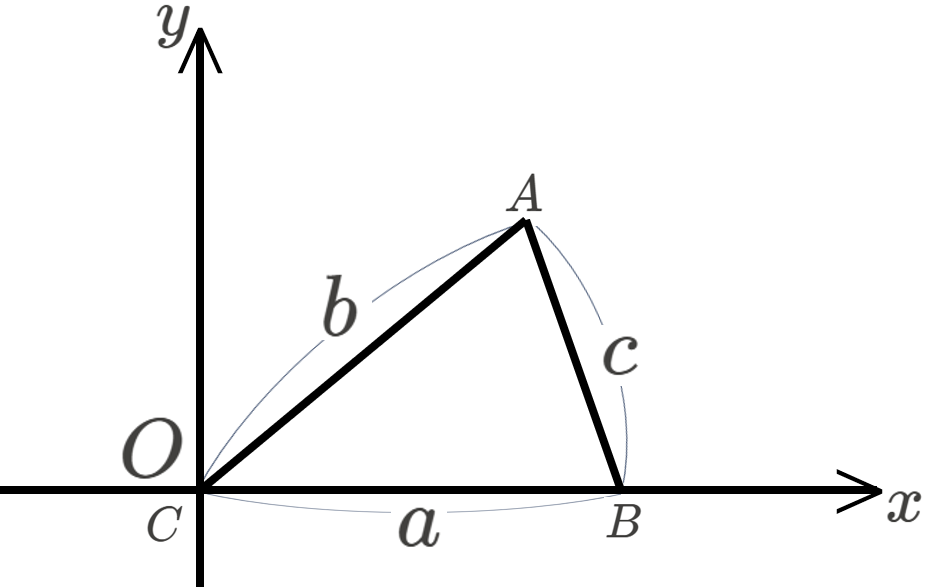
上の図のように、\(xy\) 座標平面上に点 \(A,B,C\) をとります。
点 \(A\) から \(x\) 軸に下した垂線の足を \(H\) とすると、\(\triangle AHC\) は、\(\angle AHC=90°\) の直角三角形なので、以下の等式が成り立ちます。
\[\cos C=\frac{CH}{AC}\ \Leftrightarrow\ CH=b\cos C\]
\[\sin C=\frac{AH}{AC}\ \Leftrightarrow\ AH=b\sin C\]
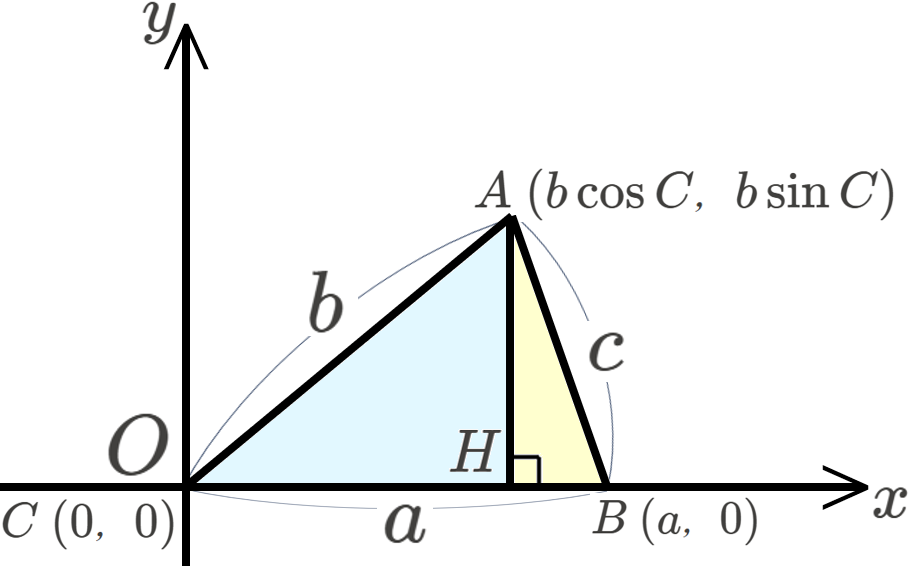
ここで、\(\triangle ABH\) に対して三平方の定理を適用すると、
\[\begin{alignat*}{3}
{AB}^{2}&={AH}^{2}+{BH}^{2} \\
&={AH}^{2}+{(BC-CH)}^{2}
\end{alignat*}\]
なので、\(AB=c\),\(AH=b\sin C\),\(BC=a\),\(CH=b\cos C\) をそれぞれ代入して、
\[{\small\begin{alignat*}{3}
{c}^{2}&={(b\sin C)}^{2}+{(a-b\cos C)}^{2} \\
&={b}^{2}\sin^{2}C+{a}^{2}-2ab\cos C+{b}^{2}\cos^{2}C \\
&={a}^{2}+{b}^{2}(\sin^{2}C+\cos^{2}C)-2ab\cos C \\
&={a}^{2}+{b}^{2}-2ab\cos C\quad(\because\ \sin^{2}C+\cos^{2}C=1)
\end{alignat*}}\]
となり、求める式が得られました。
おわりに
お疲れさまでした!今回は、正弦定理・余弦定理を確認してきました。
どちらの定理も、よく使うものではあるものの、導出の方法までは知らなかった、という方もいらっしゃったのではないでしょうか。
見てきた通り、どちらも以下の定理を利用して比較的簡単に導出できます。ぜひこの機会に、導出の流れを抑えておきましょう!
- 正弦定理は、円周角の定理(と、その逆)
- 余弦定理は、(\(xy\) 平面で)三平方の定理
ちなみに、正弦定理は、「\(=2R\)」の部分を隠すと、
\[\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}\]
\[\Leftrightarrow\ \sin A\ :\ \sin B\ :\ \sin C=a\ :\ b\ :\ c\]
となり、これは、\(\sin\) の値と、向かい合う辺の長さの比は等しい、という性質を表しています。
例えば、以下のような問題では、この性質を利用することになりますので、ぜひ合わせて意識しておきましょう!
- 三角形の3つの角と、2つの辺の長さがわかっているとき、残りの辺の長さを求める
- 三角形の2つの角と、3つの辺の長さがわかっているとき、残りの角の大きさを求める
【正弦定理】
\(\triangle ABC\) の外接円の半径を \(R\) とすると、以下の等式が成り立つ。
\[\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R\]
\[\sin A\ :\ \sin B\ :\ \sin C=a\ :\ b\ :\ c\]
(\(a\),\(b\),\(c\) は各々、角 \(A\),\(B\),\(C\) に向かい合う辺の長さ)
【余弦定理】
\(\triangle ABC\) において、以下の等式が成り立つ。
\({a}^{2}={b}^{2}+{c}^{2}-2bc\cos A\)
\({b}^{2}={c}^{2}+{a}^{2}-2ca\cos B\)
\({c}^{2}={a}^{2}+{b}^{2}-2ab\cos C\)
(\(a\),\(b\),\(c\) は各々、角 \(A\),\(B\),\(C\) に向かい合う辺の長さ)




コメント