\(\sin18\)°・\(\cos18\)°の求め方

今回は、\(\sin18\)°・\(\cos18\)°の求め方を解説します。

この「\(18\)°」という角、「なんとなく中途半端な角だなー」と思われる方もいらっしゃるかもしれません。

しかし、実は、大学入試では、結構よく聞かれている角度です。
というのも、\(18\)°\(=90\)°\(\div5\) であり、\(\sin90\)°\(=1\) なので、以下のような問題が簡単に作りやすいのです。

• \(\sin5\theta=1\) を求める問題（三角方程式・三角不等式）
  \(5\theta=90\)°\(+360\)°\(\times n\) から、\(\theta\) を求めると、\(18\)° が現れる。
• \(\sin\) の5次関数
  2倍角の公式・3倍角の公式を合わせることで、\(\sin\) の5次式が現れる。\(\sin18\)°\(=t\) と置くことで、\(t\) の5次関数として増減や、解の個数を調べさせる。

このように、「\(18\)°」という角は、結構よく現れるものなのですが、実は、比較的簡単に、\(\sin，\)\(\cos\) の値を求めることができます。

特に、\(\sin\) の5次関数に関する問題では、最後に、ズバリ「\(\sin18\)°を求めよ」というような問題が出題される可能性もあり、今回解説する方法を知っていると、ちょっとだけ有利になるかもしれません。

ぜひ、「\(18\)°」という特別な角について、理解を深めていきましょう。

解説

それでは、早速、\(\sin18\)°・\(\cos18\)°の求め方を見ていきましょう。

\(\sin18\)°

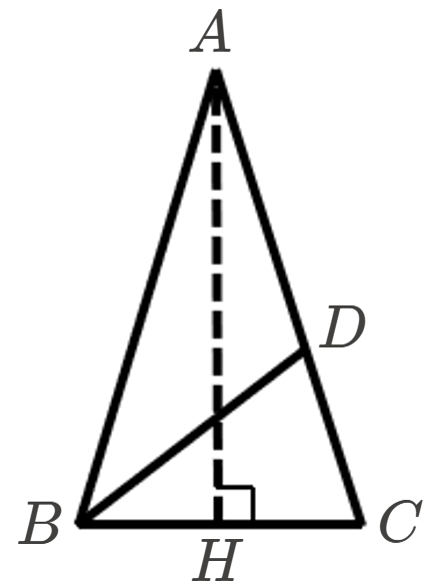
上の図のように、\(AB=AC，\)\(\angle A=36\)° の二等辺三角形 \(ABC\) を考えます。

このとき、\(\angle A=36\)°なので、\((180\)°\(-36\)°\()\div 2=72\)°から、\(\angle B=\angle C=72\)°となります。

ここで、\(\angle B\) の二等分線と、辺 \(AC\) の交点を点 \(D\) とすると、\(\angle ABC=72\)°より、\(\angle ABD=36\)°となります。
よって、\(\angle DAB=\angle DBA=36\)°のため、\(\triangle DAB\) は、\(DA=DB\) の二等辺三角形であることがわかります。

一方で、\(\angle ABC=72\)°より、\(\angle CBD=36\)°のため、\(\angle BAC=\angle CBD=36\)°。

また、\(\angle ACB=\angle BCD\) で共通なので、

\(\triangle ABC\) と \(\triangle BCD\) は、2つの角が等しいため、相似

ということがわかります。

\(\triangle ABC\) と \(\triangle BCD\) の相似比を考えると、

\[\begin{alignat*}{3}
&AB:BC=BC:CD \\
\Longleftrightarrow\ &AB:BC=BC:(AC-DA) \\
\stackrel{\mathrm{(※)}}{\Longleftrightarrow}\ &AB:BC=BC:(AB-BC) \\
\Longleftrightarrow\ &AB\cdot(AB-BC)={BC}^{2} \\
\Longleftrightarrow\ &{AB}^{2}-AB\cdot BC-{BC}^{2}=0
\end{alignat*}\]

これを、\(AB\) についての2次方程式とみて解くと、

\[\begin{alignat*}{3}
AB&=\frac{BC\pm\sqrt{{BC}^{2}-4{BC}^{2}}}{2} \\
&=\frac{BC\pm\sqrt{5}BC}{2}\ (\because\ BC>0) \\
&=BC\cdot\frac{\sqrt{5}+1}{2}・・・①\ (\because\ AB>0)
\end{alignat*}\]

ここで、点 \(A\) から辺 \(BC\) に下した垂線の足を \(H\) とすると、\(\triangle ABC\) は二等辺三角形なので、\(BH=HC\)。

したがって、\(BH=\frac{BC}{2}\) とわかります。（②）

また、\(\angle BAH=\angle CAH\) なので、\(\angle BAH=\frac{\angle BAC}{2}=\frac{36°}{2}=18\)°となります。（③）

直角三角形 \(ABH\) で、\(\sin\) を考えると、\(\sin \angle BAH=\frac{BH}{AB}\)

\[\begin{alignat*}{3}
\therefore\ \sin18°&=\frac{\frac{BC}{2}}{BC\cdot\frac{\sqrt{5}+1}{2}}\ (\because\ ①②③) \\
&= \frac{\frac{BC}{2}\times\frac{2}{BC}}{BC\cdot\frac{\sqrt{5}+1}{2}\times\frac{2}{BC}}\\
&=\frac{1}{\sqrt{5}+1} \\
&=\frac{\sqrt{5}-1}{(\sqrt{5}+1)(\sqrt{5}-1)} \\
&=\frac{\sqrt{5}-1}{5-1} \\
\end{alignat*}\]

\[\therefore\ \sin18°=\frac{\sqrt{5}-1}{4}\]

と求めることができました。

\(\cos18\)°

次に、上で求めた、\(\sin18°=\frac{\sqrt{5}-1}{4}\) と、三角比の基本性質「\(\sin^{2}\theta+\cos^{2}\theta=1\)」を利用して、\(\cos18\)°を求めていきます。

なお、三角比の基本性質については、こちらのページを参照してください

三角比の基本性質より、\(\cos^{2}18°=1-\sin^{2}18°\)

\(0°<\theta<90°\) の範囲では、\(\cos\theta>0\) であることに注意すると、

\[\begin{alignat*}{3}
\cos18°&=\sqrt{1-\sin^{2}18°} \\
&=\sqrt{1-{\Bigl(\frac{\sqrt{5}-1}{4}\Bigr)}^{2}} \\
&=\sqrt{\frac{16-(5-2\sqrt{5}+1)}{{4}^{2}}} \\
&=\sqrt{\frac{10+2\sqrt{5}}{{4}^{2}}}
\end{alignat*}\]

\[\therefore\ \cos18°=\frac{\sqrt{10+2\sqrt{5}}}{4}\]

（ルートの中にルートが含まれていて、少々気持ち悪い形になりますが、これ以上はきれいにできません）

ちなみに、電卓を使って計算してみると、以下のようになります。

• \(\sin18\)°\(=\frac{\sqrt{5}-1}{4}=0.309016994\dots\)
• \(\cos18\)°\(=\frac{\sqrt{10+2\sqrt{5}}}{4}=0.951056516\dots\)

\(90\)°→\(0\)°に近づくにつれ、

• \(\sin\)：\(1\)→\(0\)へと、\(0\)に近づく
• \(\cos\)：\(0\)→\(1\)へと、\(1\)に近づく

ということを考えると、\(18\)°は、\(0\)°に比較的近い角度のため、「確かにそんなもんかな」ということがわかります。

おわりに

今回は、\(\sin18\)°・\(\cos18\)°の求め方を解説しました。

\(18\)°や \(18\) の倍数の角度、というのは、何倍かすると有名角になる上、そこまで覚えている人も多くはないと思われ、入試ではかなり狙われやすい角度になります。

ぜひ、\(\sin18\)°・\(\cos18\)°の値自体を覚えるというよりも、二等辺三角形を作って、、、という導出の流れを、今一度復習いただき、出題された場合に備えておきましょう！