\(\sum\)シグマの公式（累乗の和）

解説

\(0\) 乗の場合

ある数を \(0\) 乗すると、\(1\) になることに注意すると、\[\sum^{n}_{k=1}{k}^{0}=\sum^{n}_{k=1}1\]となります。これを、シグマ \(\sum\)を使わずに表すと、

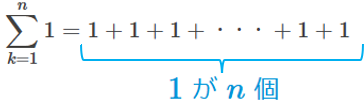
右辺には、\(1\) が \(n\) 個並ぶため、\[\sum^{n}_{k=1}{k}^{0}=\sum^{n}_{k=1}1=n\]が導けました。

\(1\) 乗の場合

以下の2つの式を考えます。

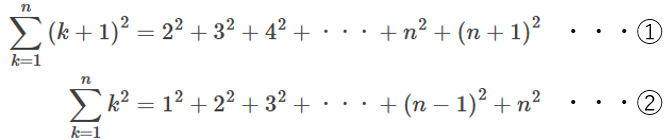
①②の左辺について、①－②をすると、

\[\begin{alignat*}{3}
&\sum^{n}_{k=1}{(k+1)}^{2}-\sum^{n}_{k=1}{k}^{2} \\
&=\sum^{n}_{k=1}({k}^{2}+2k+1)-\sum^{n}_{k=1}{k}^{2} \\
&=\biggr(\sum^{n}_{k=1}{k}^{2}+2\sum^{n}_{k=1}k+\sum^{n}_{k=1}1\biggr)-\sum^{n}_{k=1}{k}^{2}\quad&(※1)\\
&=2\sum^{n}_{k=1}k+\sum^{n}_{k=1} \\
&=2\sum^{n}_{k=1}k+n\quad・・・③&(※2)
\end{alignat*}\]
(※1)こちらの式変形は、次の記事を参照してください

(※2)こちらの式変形には、上の0乗の場合の結果を利用しています

ここで、改めて、①②の式を見てみます。
\(2\) 乗される数（＝底）の等しい項が縦に並ぶようにして、両辺を①-②すると、

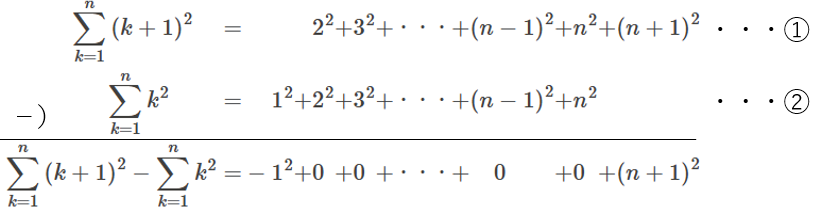
このように、右辺は、

間の項が全て \(0\) になり、\(-{1}^{2}+{(n+1)}^{2}\)　だけ残る

ことがわかります。この式の左辺に、③の結果を代入して、

\[\begin{alignat*}{3}
&2\sum^{n}_{k=1}k+n=-{1}^{2}+{(n+1)}^{2} \\
\Leftrightarrow\quad&2\sum^{n}_{k=1}k=-1+({n}^{2}+2n+1)-n \\
\Leftrightarrow\quad&2\sum^{n}_{k=1}k=n(n+1) \\
\Leftrightarrow\quad&\sum^{n}_{k=1}k=\frac{1}{2}n(n+1)
\end{alignat*}\]

が得られました。

なお、\(1\) 乗の場合は、初項 \(a=1\) ，公差 \(d=1\) の等差数列とみて、等差数列の一般項の公式から導くこともできます。
等差数列の一般項の公式は、こちらの記事をご覧ください。

\(2\) 乗の場合

続いて、\(2\) 乗の場合を考えます。発想は、\(1\) 乗の場合と同じです。
まず、以下の2つの式を考え、左辺の④-⑤と、右辺の④-⑤を計算します。

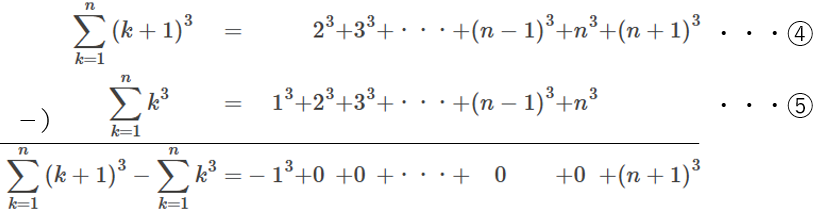
まず、右辺については、
\[\begin{alignat*}{3}
右辺&=-1+({n}^{3}+3{n}^{2}+3n+1) \\
&={n}^{3}+3{n}^{2}+3n\qquad・・・⑥
\end{alignat*}\]

次に、左辺について計算すると、
\[\begin{alignat*}{3}
&\sum^{n}_{k=1}{(k+1)}^{3}-\sum^{n}_{k=1}{k}^{3} \\
&=\sum^{n}_{k=1}({k}^{3}+3{k}^{2}+3k+1)-\sum^{n}_{k=1}{k}^{3} \\
&={\small \biggr(\sum^{n}_{k=1}{k}^{3}+3\sum^{n}_{k=1}{k}^{2}+3\sum^{n}_{k=1}k+\sum^{n}_{k=1}1\biggr)-\sum^{n}_{k=1}{k}^{3}} \\
&=3\sum^{n}_{k=1}{k}^{2}+3\sum^{n}_{k=1}k+\sum^{n}_{k=1} \\
&=3\sum^{n}_{k=1}{k}^{2}+3\cdot\frac{1}{2}n(n+1)+n\quad(※3)\\
&=3\sum^{n}_{k=1}{k}^{2}+\frac{3}{2}{n}^{2}+\frac{5}{2}n\quad・・・⑦
\end{alignat*}\]
(※3)こちらの式変形には、上の0乗の場合・1乗の場合の結果を利用しています

⑥=⑦より、
\[\begin{alignat*}{3}
&{\small {n}^{3}+3{n}^{2}+3n=3\sum^{n}_{k=1}{k}^{2}+\frac{3}{2}{n}^{2}+\frac{5}{2}n} \\
\Leftrightarrow\quad&{\small 3\sum^{n}_{k=1}{k}^{2}=({n}^{3}+3{n}^{2}+3n)-(\frac{3}{2}{n}^{2}+\frac{5}{2}n)} \\
\Leftrightarrow\quad&3\sum^{n}_{k=1}{k}^{2}=\frac{1}{2}(2{n}^{3}+3{n}^{2}+n) \\
\Leftrightarrow\quad&3\sum^{n}_{k=1}{k}^{2}=\frac{1}{2}n(n+1)(2n+1) \\
\Leftrightarrow\quad&\sum^{n}_{k=1}{k}^{2}=\frac{1}{6}n(n+1)(2n+1)
\end{alignat*}\]
が得られました。

\(3\) 乗の場合

続いて、\(3\) 乗の場合を考えます。こちらも発想は、\(1\) 乗・\(2\) 乗の場合と同じです。（\(1\) 乗・\(2\) 乗と同じなので、お急ぎの方は、次の章まで飛ばしてください）

まず、以下の2つの式を考え、左辺の⑧-⑨と、右辺の⑧-⑨を計算します。
（ポイントは、\(3\) 乗の和なので、\(3+1=4\) 乗の引き算を考えることです）

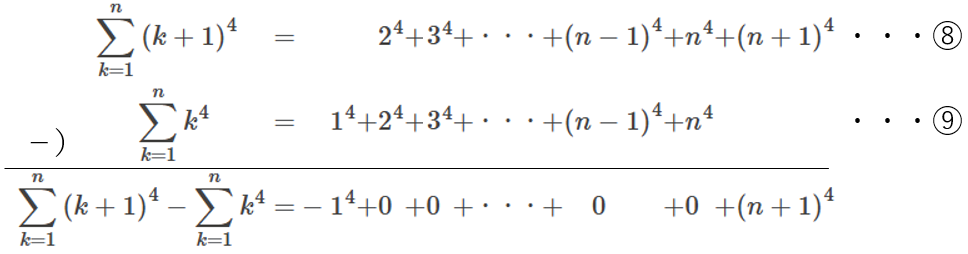
まず、右辺については、
\[\begin{alignat*}{3}
右辺&=-1+({n}^{4}+4{n}^{3}+6{n}^{2}+4n+1) \\
&={n}^{4}+4{n}^{3}+6{n}^{2}+4n\qquad・・・⑩
\end{alignat*}\]

次に、左辺について計算すると、
\[\begin{alignat*}{3}
&\sum^{n}_{k=1}{(k+1)}^{4}-\sum^{n}_{k=1}{k}^{4} \\
&=\sum^{n}_{k=1}({k}^{4}+4{k}^{3}+6{k}^{2}+4k+1)-\sum^{n}_{k=1}{k}^{3} \\
&={\scriptsize\biggr(\sum^{n}_{k=1}{k}^{4}+4\sum^{n}_{k=1}{k}^{3}+6\sum^{n}_{k=1}{k}^{2}+4\sum^{n}_{k=1}k+\sum^{n}_{k=1}1\biggr)-\sum^{n}_{k=1}{k}^{3}} \\
&=4\sum^{n}_{k=1}{k}^{3}+6\sum^{n}_{k=1}{k}^{2}+4\sum^{n}_{k=1}k+\sum^{n}_{k=1} \\
&={\scriptsize 4\sum^{n}_{k=1}{k}^{3}+6\cdot\frac{1}{6}n(n+1)(2n+1)+4\cdot\frac{1}{2}n(n+1)+n\quad(※4)} \\
&=4\sum^{n}_{k=1}{k}^{3}+2{n}^{3}+5{n}^{2}+4n\quad・・・⑪
\end{alignat*}\]
(※4)こちらの式変形には、上の0乗の場合・1乗の場合・2乗の場合の結果を利用しています

⑩=⑪より、
\[\begin{alignat*}{3}
&{\scriptsize {n}^{4}+4{n}^{3}+6{n}^{2}+4n=4\sum^{n}_{k=1}{k}^{3}+2{n}^{3}+5{n}^{2}+4n} \\
\Leftrightarrow\quad&{\scriptsize 4\sum^{n}_{k=1}{k}^{3}=({n}^{4}+4{n}^{3}+6{n}^{2}+4n)-(2{n}^{3}+5{n}^{2}+4n)} \\
\Leftrightarrow\quad&4\sum^{n}_{k=1}{k}^{3}={n}^{4}+2{n}^{3}+{n}^{2} \\
\Leftrightarrow\quad&4\sum^{n}_{k=1}{k}^{3}=\{{n(n+1)}\}^{2} \\
\Leftrightarrow\quad&\sum^{n}_{k=1}{k}^{3}=\biggr\{\frac{1}{2}{n(n+1)}\biggr\}^{2}
\end{alignat*}\]
が得られました。

（発展）\(4\) 乗以降の累乗の和

今まで見てきた通り、

\(m\) 乗の和を求める場合、\((m+1)\) 乗の和を考え、引き算する

ことがポイントです。

ただ、\(3\) 乗まで計算しただけでも、かなりの計算量になってしまい、\(4\) 乗、\(5\) 乗、、、と考えるのは気が遠くなりそうです。。。
そこで、現在では、この算出方法をより一般化し、（一応、）任意の自然数 \(m\) に対して公式が発明されています。（ファウルハーバーの公式）

、、、が、こちらの公式は非常に複雑な形をしており、とても試験の現場で使えるようなものではありません。
そこで、もし万が一、\(4\) 乗以降の累乗の和を求める問題が出題されてしまった場合は、以下の手順で計算するようにしましょう。（そんな鬼畜な問題は出ない気もしますが）

• 次の2つを書き出す\[\sum^{n}_{k=1}{(k+1)}^{m+1}　と　\sum^{n}_{k=1}{k}^{m+1}\]
• \(m+1\) 乗される数（＝底）の等しい項が縦に並ぶようにして、両辺を引き算する
  （このとき、左辺は、ちょうど、\((m+1)\) 乗のシグマ \(\sum\) が消えることがポイント）
• 左辺について、\(0\) 乗～ \((m-1)\) 乗の項は、同じことを何度も繰り返せば、シグマ \(\sum\) が無くなった、\(n\) だけの式で表せる
• 式を整理すれば、\(f(n)\)（＝\(n\) の \((m+1)\) 次式）を用いて、\[\sum^{n}_{k=1}{k}^{m}=f(n)\]の形で表せる

ちなみに、上記の計算で得られた \(m\) 乗の和について、実際に計算するのは非常に大変ですが、以下のことは、数学的帰納法ですぐに確かめることができます。

• \(m\) 乗の和は、\(n\) の \((m+1)\) 次式で表すことができる
• その \(n\) の \((m+1)\) 次式において、\((m+1)\) 次の項の係数は、\[\frac{1}{m+1}\]

興味がある方は、ぜひ、お試しください！

おわりに

今回は、シグマ \(\sum\) の公式として、累乗の和の計算を見てきました。

ご覧いただいたように、乗数が上がるにつれ、計算量がエグいことになるのですが、一応、頑張れば計算で出せないことはない、ということがわかっていただけたかと思います。

試験の現場で、万が一にも公式を忘れてしまった場合に備え、受験生の皆さんは、1度は手を動かして、 \(3\) 乗くらいまでは公式を導出してみることをオススメします。
特に、\(m\) 乗の和を求める場合、\((m+1)\) 乗の和を考えて、引き算すれば、求めたい項が出てくる、という感覚をつかんでいただけると思います。

ぜひ、公式の導出を通じて、累乗の和の公式を自分のものにしてください！