【定数と\(\sum\)の関係】
\(\sum\) と、定数 \(a\) は入替可能\[\sum^{n}_{k=1}a\cdot{a}_{k}=a\cdot\sum^{n}_{k=1}{a}_{k}\]
【複数の数列と\(\sum\)の関係】
足し算・引き算をバラバラにできる\[\sum^{n}_{k=1}({a}_{k}+{b}_{k})=\sum^{n}_{k=1}{a}_{k}+\sum^{n}_{k=1}{b}_{k}\]
(※)これらを1つにまとめると、
定数 \(a\),\(b\),数列 \(\{{a}_{n}\}\{{b}_{n}\}\) に対し、
\[\begin{alignat*}{3}
\sum^{n}_{k=1}(a\cdot{a}_{k}&+b\cdot{b}_{k}) \\
&=a\cdot\sum^{n}_{k=1}{a}_{k}+b\cdot\sum^{n}_{k=1}{b}_{k}
\end{alignat*}\]
と書けます。(線形性)
解説
定数と\(\sum\)の関係
数列 \(\{{a}_{n}\}\) に対して、各項を \(a\) 倍した数列 \(\{a\cdot {a}_{n}\}\) を考えると、第 \(1\) 項から第 \(n\) 項までの和は、次のように表せます。
\[\begin{alignat*}{3}
&\sum^{n}_{k=1}a\cdot{a}_{k} \\
&=a\cdot{a}_{1}+a\cdot{a}_{2}+・・・+a\cdot{a}_{n-1}+a\cdot{a}_{n}
\end{alignat*}\]
右辺は、\(a\) で括れるので、
\[\begin{alignat*}{3}
\sum^{n}_{k=1}&a\cdot{a}_{k} \\
&=a\cdot({a}_{1}+{a}_{2}+・・・+{a}_{n-1}+{a}_{n})
\end{alignat*}\]
となり、右辺のカッコの中は
\[\sum^{n}_{k=1}{a}_{k}\]
なので、
\[\sum^{n}_{k=1}a\cdot{a}_{k}=a\cdot\sum^{n}_{k=1}{a}_{k}\]
が導けました。
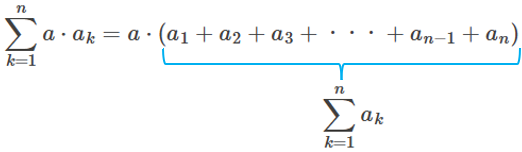
複数の数列と\(\sum\)の関係
数列 \(\{{a}_{n}\}\{{b}_{n}\}\) に対し、それらを足し合わせた数列 \(\{{a}_{n}+{b}_{n}\}\) のシグマ \(\sum\) を考えると、
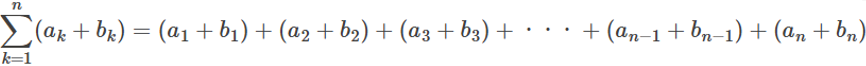
となります。
そして、足し算の順番は入れ替えても結果は変わらないので(※)、右辺を \(\{{a}_{n}\}\) と \(\{{b}_{n}\}\) の部分に分けると、次のように書き換えられます。
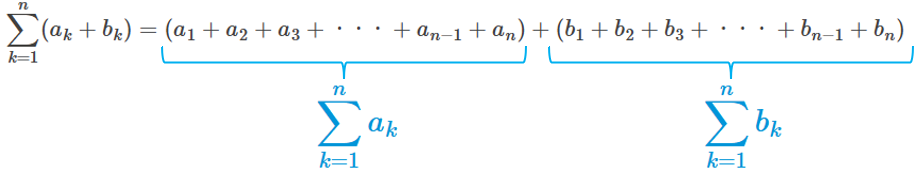
したがって、
\[\sum^{n}_{k=1}({a}_{k}+{b}_{k})=\sum^{n}_{k=1}{a}_{k}+\sum^{n}_{k=1}{b}_{k}\]
が得られました。
(※)今回の議論は、有限個の項を想定しているため、足し算の順番の入れ替えが可能と、簡単に認めています。
無限個の項の和を考える場合には、順番を入れ替え可能か、より丁寧に確認する必要があります。
(補足)2つの関係を、1つにまとめる
上で得られた2つの関係ですが、他の教科もあるし、なるべく覚えることを少なくしたいところ・・・
そこで、2つの関係を、1つにまとめることを考えます。
定数 \(a\),\(b\),数列 \(\{{a}_{n}\}\{{b}_{n}\}\) に対し、
\[\sum^{n}_{k=1}(a\cdot{a}_{k}+b\cdot{b}_{k})\]
を式変形すると、
\[\begin{alignat*}{3}
\sum^{n}_{k=1}(&a\cdot{a}_{k}+b\cdot{b}_{k}) \\
&=\sum^{n}_{k=1}a\cdot{a}_{k}+\sum^{n}_{k=1}b\cdot{b}_{k}\qquad(\because 2つ目の関係「複数の数列と \sum の関係」より) \\
&=a\cdot\sum^{n}_{k=1}{a}_{k}+b\cdot\sum^{n}_{k=1}{b}_{k}\qquad(\because 1つ目の関係「定数と \sum の関係」より)
\end{alignat*}\]
となり、1つの式にまとめることができました。この式から、シグマ \(\sum\) の計算をするときは、
- 添え字に関係ない定数を、シグマ \(\sum\) の外に出せる
- シグマ \(\sum\) の中の足し算・引き算を、バラバラにできる
ということがわかりました。(難しい言葉で、このような性質を 線形性がある といいます)
おわりに
今回は、定数と\(\sum\)の関係・複数の数列と\(\sum\)の関係を解説しました。
これらの関係については、受験数学の中では、式変形を行う中で、当然に出てくるものとなります。
ぜひ、理解できるまで何度もこのページを読み返して、脊髄反射で式変形ができるように練習してみてください!
ちなみに、補足として記載した「線形性」ですが、少し慣れている人であれば、どちらも当たり前じゃない?と思われた方もいらっしゃるかもしれません。
でも、実は、この線形性は当たり前に成り立つものではありません。
例えば、\(f(x)={x}^{2}\) という関数 \(f\) を考えると、
1つ目の関係(定数を外に出せる)は、
\[\begin{alignat*}{3}
f(ax)&={(ax)}^{2}={a}^{2}\cdot{x}^{2} \\
&\ne a\cdot{x}^{2}=a\cdot f(x)
\end{alignat*}\]
2つ目の関係(足し算・引き算をバラバラにできる)は、
\[\begin{alignat*}{3}
f(x+y)&={(x+y)}^{2}={x}^{2}+2xy+{y}^{2} \\
&\ne{x}^{2}+{y}^{2}=f(x)+f(y)
\end{alignat*}\]
となり、線形性の2つの関係は、いずれも満たさないことがわかります。
線形性については、このページの趣旨を大きく飛び出してしまうため、こちらでの詳しい解説は省略しますが、興味がある方は、ぜひコメントよりご連絡いただけると嬉しいです!
解説ページを作成するようにします。
【定数と\(\sum\)の関係】
\(\sum\) と、定数 \(a\) は入替可能
\[\sum^{n}_{k=1}a\cdot{a}_{k}=a\cdot\sum^{n}_{k=1}{a}_{k}\]
【複数の数列と\(\sum\)の関係】
足し算・引き算をバラバラにできる
\[\sum^{n}_{k=1}({a}_{k}+{b}_{k})=\sum^{n}_{k=1}{a}_{k}+\sum^{n}_{k=1}{b}_{k}\]
(※)これらを1つにまとめると、
定数 \(a\),\(b\),数列 \(\{{a}_{n}\}\{{b}_{n}\}\) に対し、
\[\begin{alignat*}{3}
\sum^{n}_{k=1}(a\cdot{a}_{k}&+b\cdot{b}_{k}) \\
&=a\cdot\sum^{n}_{k=1}{a}_{k}+b\cdot\sum^{n}_{k=1}{b}_{k}
\end{alignat*}\]
と書けます。(線形性)



コメント