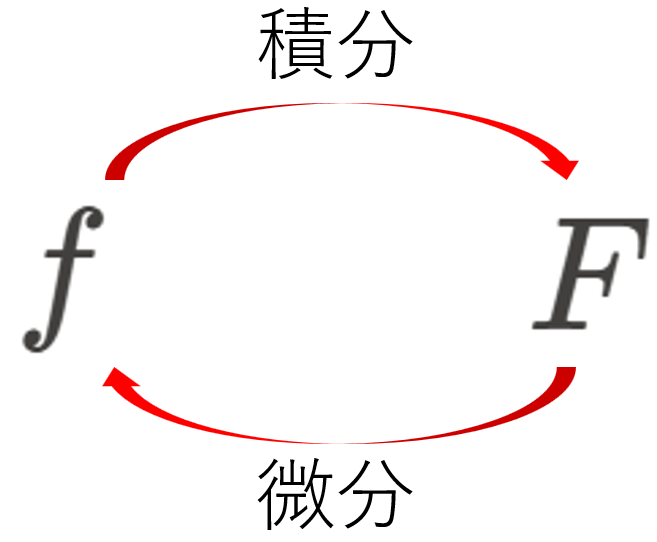
積分と面積の関係
関数の積分が面積になることの意味
【\({x}^{n}\) の積分】
\(0\) 以上の整数 \(n\) に対して、
\[\int{x}^{n}\ dx=\frac{1}{n+1}{x}^{n+1}+C\quad(C は積分定数)\]
今回は、積分と面積の関係についてみていきます。
なんとなく、
- 積分は、微分の逆の計算
- 積分をすると、面積が計算できる
という性質を覚えていても、
- なぜこのような性質があるか
- これらの性質の間にどんな関係があるか
までは知らない、という方も多いと思います。
実は、これらの性質は、
片方を定義すると、もう片方の性質が得られる
という関係にあり、「同値」です。つまり、
- 積分を「微分の逆演算」と定義すると、「面積が求められる」という性質が導かれる
- 積分を「面積(※)を求めること」と定義すると、「微分の逆演算」という性質が導かれる
という関係にあります。
※厳密には「リーマン和」と言います
今回は、この1・2を、両方とも見ていきます。
なお、2については、大学の解析学で学ぶ内容のため発展としていますが、高校生の方でも理解できるように解説していきますので、ぜひ気楽に読んでいただければと思います。
※なお、わかりやすさを重視するため、難しい計算は極力省いています。それにより、多少厳密さに欠ける点がありますがご了承ください
解説
(事前準備)「積分は、微分の逆演算」の意味を確認する
今回は、公式の導出に当たり、積分が微分の逆演算であるということを利用します。そこで、先に、この意味を、確認してみましょう。
なお、ここでは、イメージをつかむことを優先し、少々ざっくりとした解説をしています。(正確な理解には、大学数学の理解が必要になります。。)
ぜひ、「確かに逆演算になりそうだ」という、「気持ち」の部分の理解をしていただけるとありがたいです。
(以下、このページでは、積分定数を \(C\) と記載します)
今回は、「積分とは何か」を見ていきたいと思います。
高校では、「微分の逆演算」と定義することが多いと思います。そして、積分(=微分の逆演算)をすると、その性質として、面積が求められる
一方で、大学以降の学習では、積分とは、「面積のこと」と定義します(厳密には、リーマン和の極限)このように定義すると、その性質として、「微分の逆演算」であることがわかります。
これらのことから、「面積を求めること」と「微分の逆演算」は同じこと(同値)とわかります。
積分とは、微分の逆演算である、と定義します。
すると、
\[F(x)=\int f(x)\ dx\stackrel{\mathrm{def}}{\Longleftrightarrow}F'(x)=f(x)\]
ここからは、このように定義することで、
\[\int f(x)\ dx\]
という演算により、面積を求められることを確認します。
関数 \(F\) と \(f\) の間に、「関数 \(F\) を微分すると、\(f\) になる」という関係が成り立っているとします。つまり、次のように表せます。
\[F'(x)=f(x)\]
また、新たな関数 \(g\) を、以下の条件を満たすように用意します。
<条件>
区間 \([{x}_{0},x]\) において、\(y=g(x)\) と \(x\) 軸で囲まれた面積が \(F(x)\) となる。
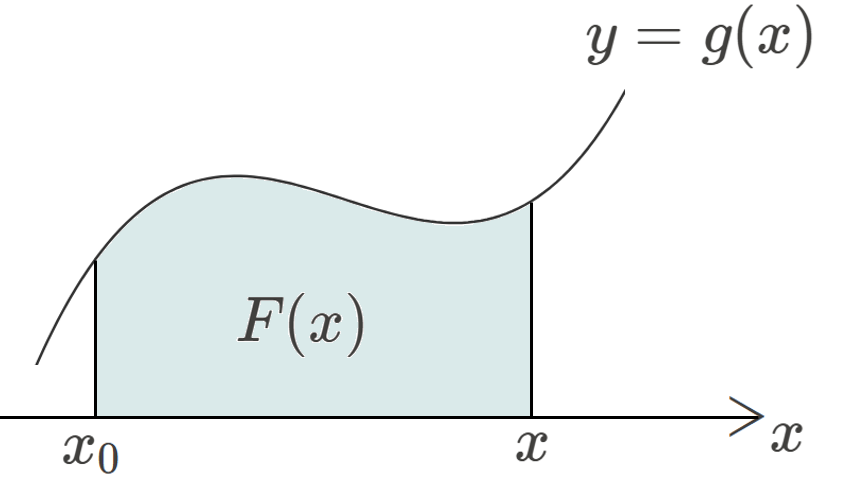
ここで、上の図の、右端 \(x\) から、わずかな量 \(\Delta x\) だけ右にずらしたときの、\(F\) の変化を調べてみます。
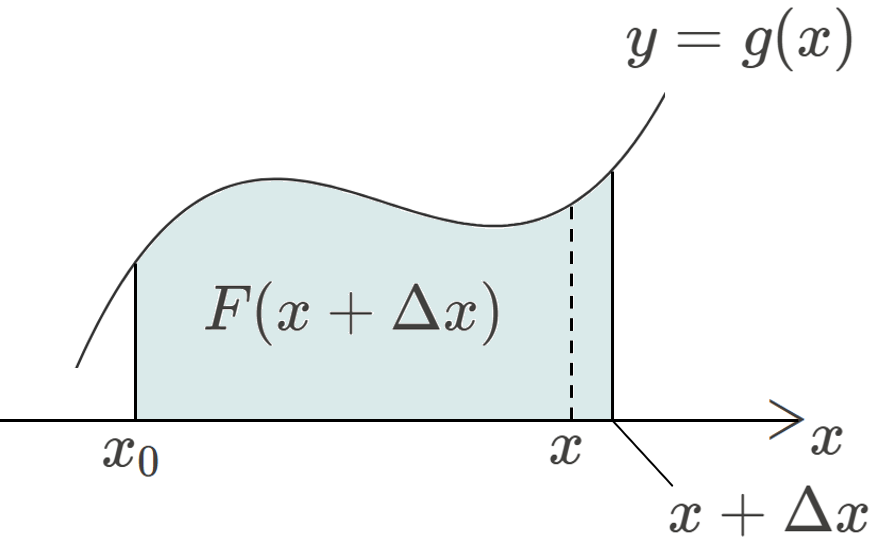
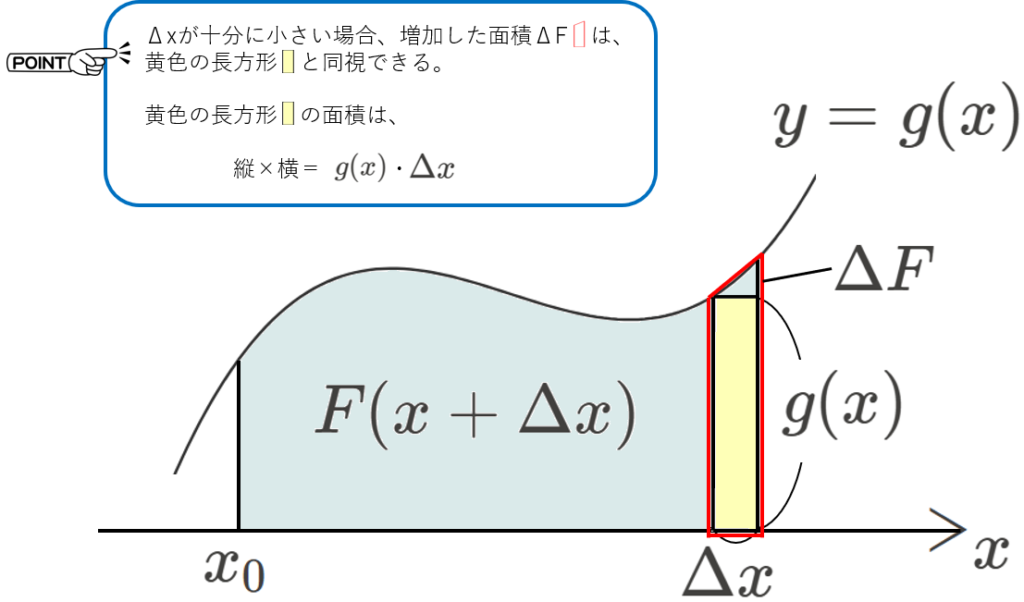
\(\Delta x\) は、わずかな量であるため、増加した面積 \(\Delta F\) は、以下のように近似することができます。(\(\thickapprox\) は、ニアリーイコールの意味です。)
\[\begin{alignat*}{3}
\Delta F\ &\thickapprox\ g(x)\cdot\{(x+\Delta x)-x\} \\
&=\ g(x)\cdot\Delta x
\end{alignat*}\]
\(\Delta F\ \thickapprox\ g(x)\cdot\Delta x\) の両辺を \(\Delta x\) で割ると、
\[\frac{\Delta F}{\Delta x}\thickapprox\ g(x)\quad・・・①\]
そして、上の図を見ていただくと、\(\Delta x\) を限りなく小さくする(=\(\Delta x\to 0\) の極限をとる)と、赤枠の \(\Delta F\) の面積は、黄色の長方形 \(g(x)\cdot\Delta x\) と等しくなることがイメージできると思います。
(\(\Delta x\) が \(0\) に近づくにつれて、斜めの部分が平らになっていく)
そのため、①の式で、左辺の \(\Delta x\to 0\) の極限を考えると、
\[\lim_{\Delta x\to 0}\frac{\Delta F}{\Delta x}=g(x)\quad・・・②\]
とできます。ここで、左辺の形は、微分の定義そのものであることから、②の式は、
\[F'(x)=g(x)\quad・・・③\]
と書けます。したがって、面積の関数 \(F\) を微分すると、面積を与える関数 \(g\) を得られることがわかりました。
ここで、一番最初に置いた前提を思い出したいのですが、関数 \(F\) と \(f\) の間には、「関数 \(F\) を微分すると、\(f\) になる」という関係が成り立っていて、以下のように表せたのでした。
\[F'(x)=f(x)\]
これと③を見比べれば、\(f(x)=g(x)\) であることがわかります
そして、元々、
\[F(x)=\int f(x)\ dx\stackrel{\mathrm{def}}{\Longleftrightarrow}F'(x)=f(x)\]
と定義していたため、\(\int\limits f(x)\ dx\) という演算により、面積が求められることがわかりました。
Fは面積 → 面積を微分すると、元の関数fになった
積分することと面積を求めることは同値(定義) → 積分を微分すると元の関数fになる→逆演算
\(\)\(\Delta x\to 0\) に近づけると、微分の定義から、左辺は \(F'(x)\) となります。
\[\lim_{\Delta x\to 0}\frac{\Delta F}{\Delta x}
\[F'(x)=
「積分が微分の逆演算である」というのは、関数 \(F,f\) を用いると、次の2つが同じことを言っている(同値である)という意味になります。
\[\int f(x)\ dx=F(x)+C\quad\Leftrightarrow\quad f(x)=F'(x)\]
となる
\(x\) 軸と、面積が\(F(x)\)となるような関数\(g\)を考えます
このとき、右端のbを少しだけ右にずらした時の面積の変動を考えてみましょう。
ずらした分が△xとすると、長方形の面積が増えるので、増加する面積は、△x✖️g(b+△x)とかけます。
また、F(x+b)ーF(x)
図を挿入
g=fだった
逆に言えば、積分を微分の逆演算と定義すると、積分とは面積を求めることに等しかった
ここで\(f(x)\)と\(x\)軸で囲まれた部分の面積を表す関数を\(S\)とすると、\(S\)は\(f\)によって決まる※ので、新たな関数\(g\)を使って、
\[S(x)=g(f(x))\]
と書ける。ここで、新たに追加した関数\(g\)を具体的に求めたい



コメント