【相加平均と相乗平均の関係(文字が2つの場合)】
\(x,y>0\) に対して、
\[\frac{x+y}{2}\geqq\sqrt{xy}\]
(等号成立は \(x=y\) のとき)
【(発展)相加平均と相乗平均の関係(文字が3つの場合)】
\(x,y,z>0\) に対して、
\[\frac{x+y+z}{3}\geqq\sqrt[3]{xyz}\]
(等号成立は \(x=y=z\) のとき)
【(発展)相加平均と相乗平均の関係(文字が \(n\) 個の場合)】
正の数の数列 \(\{{a}_{n}\}\) に対して、
\[\frac{1}{n}\sum_{k=1}^{n}{a}_{k}\geqq\sqrt[n]{\prod_{k=1}^{n}{a}_{k}}\]
(等号成立は \({a}_{1}=\)\(\ {a}_{2}=\)\(\ \dots=\)\(\ {a}_{n}\) のとき)
※\(\prod\) は \(\sum\) と同様に、\(k=1\) ~ \(n\) まで、\({a}_{k}\) を掛け算するという記号です
今回は、相加平均と相乗平均の関係を解説します。
こちらの関係は、文字が2つ・3つ程度の場合は、証明が比較的容易である一方で、利用できる場面が意外と多く、使いこなせると非常に便利なツールとなります。
また、難関大学の入試では、誘導付きではあるものの、n個の文字についての相加平均と相乗平均の関係を導出させるような問題も出題されているようです。
今回は、文字が2つの場合と、n個の場合で、2つずつ証明方法をご紹介していますので、ぜひたくさんの証明に触れ、理解を深めていっていただければうれしいです!
なお、分量の都合から、文字が3つの場合の証明は割愛しています。
\[\begin{alignat*}{3}
&{a}^{3}+{b}^{3}+{c}^{3}-3abc \\
&\qquad{\small=(a+b+c)({a}^{2}+{b}^{2}+{c}^{2}-ab-bc-ca)}
\end{alignat*}\]
という基本公式を変形することで、簡単に導出できますので、ぜひトライしてみてください。
(ポイントは、右辺を変形して、2乗の形を3つ作ることです)
※2025/3/13追記
こちらのページに解説を追加しましたので、答え合わせがてらご覧ください
解説
文字が2つの場合(\(\frac{x+y}{2}\geqq\sqrt{xy}\))
【相加平均と相乗平均の関係(文字が2つの場合)】
\(x,y>0\) に対して、
\[\frac{x+y}{2}\geqq\sqrt{xy}\]
(等号成立は \(x=y\) のとき)
式変形による証明
まずは、単純な式変形から、こちらの関係を導出してみましょう。
<証明>
\(x,y>0\) に対して、
\[\begin{alignat*}{3}
&{\Bigl(\frac{x+y}{2}\Bigr)}^{2}-xy \\
=&\frac{1}{{2}^{2}}\cdot\bigl\{({x}^{2}+2xy+{y}^{2})-4xy\bigr\} \\
=&\frac{1}{{2}^{2}}\cdot({x}^{2}-2xy+{y}^{2}) \\
=&{\Bigl(\frac{x-y}{2}\Bigr)}^{2}・・・①
\end{alignat*}\]
ここで、 右辺は、実数の2乗の形をしているため、右辺 \(\geqq 0\) です。
したがって、
\[{\Bigl(\frac{x+y}{2}\Bigr)}^{2}-xy={\Bigl(\frac{x-y}{2}\Bigr)}^{2}\geqq 0\]
\[\therefore\ {\Bigl(\frac{x+y}{2}\Bigr)}^{2}\geqq xy\]
\(x,y>0\) なので、
\[\frac{x+y}{2}\geqq \sqrt{xy}\]
となり、求める関係式が得られました。
また、上の証明より、等号が成立するのは、① \(=0\) の場合です。
したがって、
\[{\Bigl(\frac{x-y}{2}\Bigr)}^{2}=0\]
\[\therefore\ x=y\]
となり、等号成立の条件も確認できました。
(証明終了)
図形の性質に着目した証明
相加平均と相乗平均の関係は、いくつかの証明方法が知られており、実は、図形の性質に注目することでも証明ができます。
図形を見るだけで一目瞭然ということで、非常に芸術的な証明になりますので、ぜひ、こちらもご紹介させてください。
<証明>
下の図のように、円周上の点 \(A,\)\(B,\)\(C,\)\(P\) と、 点 \(P\) から 線分 \(AB\) に下した垂線の足 \(H\) をとり、\(AH=x,\)\(BH=y\) と置きます。
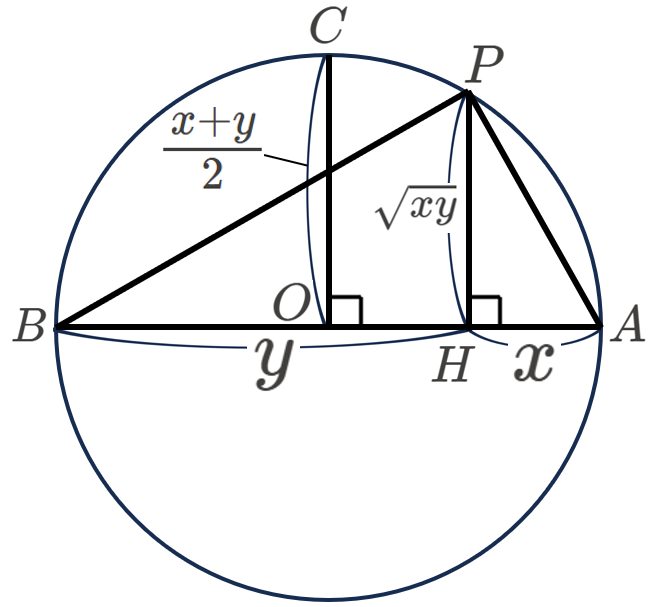
このとき、\(CO=\frac{x+y}{2},\)\(PH=\sqrt{xy}\) となることを確認します。
まず、\(CO\) について、
線分 \(AB\) は、円 \(O\) の直径であり、\(AB\)\(\ =AH+BH=\)\(\ x+y\) なので、円 \(O\) の半径は、\(\frac{x+y}{2}\) とわかります。
そして、線分 \(CO\) は、円 \(O\) の半径であることから、\(CO=\)\(\ \frac{x+y}{2}\) と導出できました。
次に、\(PH\) について、
\(\triangle PAH,\)\(\triangle PBH\) はいずれも直角三角形なので、それぞれ三平方の定理を適用すると、
- \({PA}^{2}=\)\(\ {PH}^{2}+\)\(\ {AH}^{2}\)・・・①
- \({PB}^{2}=\)\(\ {PH}^{2}+\)\(\ {BH}^{2}\)・・・②
一方で、円周角の定理より、\(\triangle PAB\) も直角三角形なので、三平方の定理を適用すると、
\[\begin{alignat*}{3}
&{AB}^{2}={PA}^{2}+{PB}^{2} \\
\Leftrightarrow\ &{(x+y)}^{2}=({PH}^{2}+{AH}^{2}) \\
&\qquad+({PH}^{2}+{BH}^{2})\ (\because\ ①②) \\
\Leftrightarrow\ &{x}^{2}+2xy+{y}^{2}=2{PH}^{2}+{x}^{2}+{y}^{2}
\end{alignat*}\]
\[\therefore\ {PH}^{2}=xy\]
したがって、\(PH=\sqrt{xy}\) と導出できました。
今、与えられた図形より、\(PH=\sqrt{xy}\) を最大にするのは、線分 \(PH\) と線分 \(CO\) が重なったときであることがわかります。
したがって、\(CO\geqq PH\Leftrightarrow\ \)\(\frac{x+y}{2}\geqq\sqrt{xy}\) であることがわかりました。
また、等号が成立するのは、点 \(H\) と点\(O\) が重なったときであり、このとき、\(x=y\) となることから、等号成立条件 \(x=y\) についても確認できました。
(証明終了)
(発展)文字が \(n\) 個の場合
ここまでで、文字が2つの場合の相加平均と相乗平均の関係を見てきましたが、実は、一般的に文字が \(n\) 個になっても成立します!
文字が \(n\) 個の場合の証明方法は、いくつか知られているものがありますが、ここでは次の2つをご紹介します。
- 1つ目は、(変則的な)数学的帰納法を利用した方法
- 2つ目は、微分を利用した少々トリッキーな方法(数学IIIが必要)
個人的には、2つ目が、非常にスマートな方法で、結構好みだったりします!
なお、証明が少々長くなってしまう上、少々発展的な内容になるため、結果だけ分かればいいよ、という方は飛ばしていいただければと思います。
数学的帰納法を用いた証明
【(発展)相加平均と相乗平均の関係(文字が \(n\) 個の場合)】
正の数の数列 \(\{{a}_{n}\}\) に対して、
\[\frac{1}{n}\sum_{k=1}^{n}{a}_{k}\geqq\sqrt[n]{\prod_{k=1}^{n}{a}_{k}}\]
(等号成立は \({a}_{1}=\)\(\ {a}_{2}=\)\(\ \dots=\)\(\ {a}_{n}\) のとき)
※\(\prod\) は \(\sum\) と同様に、\(k=1\) ~ \(n\) まで、\({a}_{k}\) を掛け算するという記号です
<証明>
こちらの証明は、以下の3段階で行います。
- 【I】\(n=2\) のときに成立すること
→通常の数学的帰納法と同じ(ドミノの最初) - 【II】\(n={2}^{p}\) のときに成立すると仮定すると、\(n={2}^{p+1}\) のときも成立すること
→【I】と合わせると、\(n=2,\)\(4,\)\(8,\)\(16,\dots\) と、\(n\) が2の累乗の場合に成立することが示される - 【III】\(n=q+1\) のときに成立すると仮定すると、\(n=q\) のときも成立すること
→【II】で示した2の累乗から、\(n\) を1ずつマイナスしても成立することが示され、結果的に、すべての自然数 \(n\) で成立する
【I】\(n=2\) のとき、前の章で、成立することを証明しました。
【II】\(n={2}^{p}\) のとき、与えられた関係が成立すると仮定すると、
\[\frac{1}{{2}^{p}}\sum_{k=1}^{{2}^{p}}{a}_{k}\geqq\sqrt[{2}^{p}]{\prod_{k=1}^{{2}^{p}}{a}_{k}}・・・①\]
(等号成立は \({a}_{1}=\)\(\ {a}_{2}=\)\(\ \dots=\)\(\ {a}_{{2}^{p}}\) のとき)
\(n={2}^{p+1}\) のとき、
\[\begin{alignat*}{3}
&\frac{1}{{2}^{p+1}}\sum_{k=1}^{{2}^{p+1}}{a}_{k} \\
=&{\small\frac{1}{{2}^{p+1}}\{({a}_{1}+\dots+{a}_{{2}^{p}})+({a}_{{2}^{p}+1}+\dots+{a}_{{2}^{p+1}})\}} \\
=&{\small\frac{1}{2}\Bigl(\frac{{a}_{1}+\dots+{a}_{{2}^{p}}}{{2}^{p}}+\frac{{a}_{{2}^{p}+1}+\dots+{a}_{{2}^{p}+{2}^{p}}}{{2}^{p}}\Bigr)} \\
=&\frac{1}{2}\Bigl(\frac{1}{{2}^{p}}\sum_{k=1}^{{2}^{p}}{a}_{k}+\frac{1}{{2}^{p}}\sum_{k=1}^{{2}^{p}}{a}_{{2}^{p}+k}\Bigr) \\
\stackrel{\mathrm{(※1)}}{\geqq}&\frac{1}{2}\Biggl(\sqrt[{2}^{p}]{\prod_{k=1}^{{2}^{p}}{a}_{k}}+\sqrt[{2}^{p}]{\prod_{k=1}^{{2}^{p}}{a}_{{2}^{p}+k}}\Biggr)\ (\because\ 仮定①) \\
\stackrel{\mathrm{(※2)}}{\geqq}&\sqrt{\sqrt[{2}^{p}]{\prod_{k=1}^{{2}^{p}}{a}_{k}}\cdot\sqrt[{2}^{p}]{\prod_{k=1}^{{2}^{p}}{a}_{{2}^{p}+k}}}\ (\because\ 【I】n=2の場合) \\
=&\sqrt{\sqrt[{2}^{p}]{({a}_{1}\cdot\dots\cdot{a}_{{2}^{p}})\cdot({a}_{{2}^{p}+1}\cdot\dots\cdot{a}_{{2}^{p}+{2}^{p}})}} \\
=&\sqrt[{2}^{p+1}]{{a}_{1}\cdot\dots\cdot{a}_{{2}^{p+1}}}=\sqrt[{2}^{p+1}]{\prod_{k=1}^{{2}^{p+1}}{a}_{k}}
\end{alignat*}\]
\[\therefore\ \frac{1}{{2}^{p+1}}\sum_{k=1}^{{2}^{p+1}}{a}_{k}\geqq\sqrt[{2}^{p+1}]{\prod_{k=1}^{{2}^{p+1}}{a}_{k}}\]
となり、\(n={2}^{p+1}\) のときも求める関係式が得られました。
また、等号成立は、(※1)(※2)で、ともに等号成立する場合です。
(※1)では、仮定①より、
- \({a}_{1}=\)\(\ {a}_{2}=\)\(\ \dots=\)\(\ {a}_{{2}^{p}}\)
- \({a}_{{2}^{p}+1}=\)\(\ {a}_{{2}^{p}+2}=\)\(\ \dots=\)\(\ {a}_{{2}^{p}+{2}^{p}}\)
(※2)では、
\[\sqrt[{2}^{p}]{\prod_{k=1}^{{2}^{p}}{a}_{k}}=\sqrt[{2}^{p}]{\prod_{k=1}^{{2}^{p}}{a}_{{2}^{p}+k}}\]
となり、これらから、\(n={2}^{p+1}\) のときの等号成立は、
\({a}_{1}=\)\(\ {a}_{2}=\)\(\ \dots=\)\(\ {a}_{{2}^{p+1}}\) とわかりました。
【III】\(n=q+1\) のとき、与えられた関係が成立すると仮定すると、
\[\frac{1}{q+1}\sum_{k=1}^{q+1}{a}_{k}\geqq\sqrt[q+1]{\prod_{k=1}^{q+1}{a}_{k}}・・・②\]
(等号成立は \({a}_{1}=\)\(\ {a}_{2}=\)\(\ \dots=\)\(\ {a}_{q+1}\) のとき)
今、\(n=q+1\) のときに、上記の等式が成立すると仮定しているため、具体的に、以下のようにおいても成立します。(★)
\[{a}_{q+1}=\frac{1}{q}\sum_{k=1}^{q}{a}_{k}\]
実際に代入してみると、
\[\begin{alignat*}{3}
左辺&=\frac{1}{q+1}\sum_{k=1}^{q+1}{a}_{k} \\
&=\frac{1}{q+1}\Bigl(\sum_{k=1}^{q}{a}_{k}+{a}_{q+1}\Bigr) \\
&=\frac{1}{q+1}\Bigl(\sum_{k=1}^{q}{a}_{k}+\frac{1}{q}\sum_{k=1}^{q}{a}_{k}\Bigr) \\
&=\frac{1}{q+1}\sum_{k=1}^{q}{a}_{k}\Bigl(\frac{q+1}{q}\Bigr) \\
&=\frac{1}{q}\sum_{k=1}^{q}{a}_{k}
\end{alignat*}\]
\[\begin{alignat*}{3}
右辺&=\sqrt[q+1]{\prod_{k=1}^{q+1}{a}_{k}} \\
&=\sqrt[q+1]{\prod_{k=1}^{q}{a}_{k}\cdot{a}_{q+1}} \\
&=\sqrt[q+1]{\prod_{k=1}^{q}{a}_{k}\cdot\frac{1}{q}\sum_{k=1}^{q}{a}_{k}}
\end{alignat*}\]
仮定②より、左辺 \(\geqq\) 右辺なので、
\[\frac{1}{q}\sum_{k=1}^{q}{a}_{k}\geqq\sqrt[q+1]{\prod_{k=1}^{q}{a}_{k}\cdot\frac{1}{q}\sum_{k=1}^{q}{a}_{k}}\]
両辺を \(q+1\) 乗すると、両辺、正の値なので、
\[{\Bigl(\frac{1}{q}\sum_{k=1}^{q}{a}_{k}\Bigr)}^{q+1}\geqq\prod_{k=1}^{q}{a}_{k}\cdot\frac{1}{q}\sum_{k=1}^{q}{a}_{k}\]
両辺を \(\frac{1}{q}\sum\limits_{k=1}^{q}{a}_{k}\ (>0)\) で割ると、
\[{\Bigl(\frac{1}{q}\sum_{k=1}^{q}{a}_{k}\Bigr)}^{q}\geqq\prod_{k=1}^{q}{a}_{k}\]
両辺に \(q\) 乗根をとると、両辺、正の値なので、
\[\frac{1}{q}\sum_{k=1}^{q}{a}_{k}\geqq\sqrt[q]{\prod_{k=1}^{q}{a}_{k}}\]
となり、求める関係が得られました。
また、等号成立は、仮定②より、\({a}_{1}=\)\(\ {a}_{2}=\)\(\ \dots=\)\(\ {a}_{q}(=\)\(\ {a}_{q+1})\) のときとなります。
(証明終了)
(★)こちらの式変形は、当然、直接思いつけるものではありません。
実際の証明問題では、最終的に欲しい形から、逆算して置き換えすることになります。
微分を用いた証明 ※数学IIIが必要
【(発展)相加平均と相乗平均の関係(文字が \(n\) 個の場合)】
正の数の数列 \(\{{a}_{n}\}\) に対して、
\[\frac{1}{n}\sum_{k=1}^{n}{a}_{k}\geqq\sqrt[n]{\prod_{k=1}^{n}{a}_{k}}\]
(等号成立は \({a}_{1}=\)\(\ {a}_{2}=\)\(\ \dots=\)\(\ {a}_{n}\) のとき)
※\(\prod\) は \(\sum\) と同様に、\(k=1\) ~ \(n\) まで、\({a}_{k}\) を掛け算するという記号です
<証明>
\(f(x)={e}^{x}-(x+1)\) という関数 \(f\) を考えます。
両辺を \(x\) で微分すると、\(f'(x)={e}^{x}-1\) で、関数 \(f\) の増減表は以下のようになります。
| \(x\) | \(\dots\) | \(0\) | \(\dots\) |
| \(f'(x)\) | \(-\) | \(0\) | \(+\) |
| \(f(x)\) | \(\searrow\) | \(0\) | \(\nearrow\) |
したがって、任意の \(x\) に対して、
\[\begin{alignat*}{3}
&f(x)={e}^{x}-(x+1)\geqq 0 \\
\Leftrightarrow\ &{e}^{x}\geqq x+1・・・①
\end{alignat*}\]
という関係が得られました。(等号成立は、\(x=0\) のとき)
ここで、以下のように、\(\alpha\) という値を定義します。(ゴチャゴチャするので、見た目の簡略化のためです)
\[\begin{alignat*}{3}
&\alpha=\frac{1}{n}\sum_{k=1}^{n}{a}_{k} \\
\Leftrightarrow\ &n=\frac{1}{\alpha}\sum_{k=1}^{n}・・・②
\end{alignat*}\]
また、上記の①は、任意の \(x\) に対して成立することから、\(x=\)\( \frac{{a}_{k}}{\alpha}-\)\( 1\ \)\((1\leqq k\leqq n)\) を①に代入すると、
\[\begin{alignat*}{3}
{e}^{\frac{{a}_{k}}{\alpha}-1}&\geqq \Bigl(\frac{{a}_{k}}{\alpha}-1\Bigr)+1 \\
&=\frac{{a}_{k}}{\alpha}・・・③
\end{alignat*}\]
左辺を、\(k=1\) ~ \(n\) まで掛け合わせると、
\[\begin{alignat*}{3}
左辺&=\prod_{k=1}^{n}{e}^{\frac{{a}_{k}}{\alpha}-1} \\
&={e}^{\frac{{a}_{1}}{\alpha}-1}\cdot{e}^{\frac{{a}_{2}}{\alpha}-1}\cdot\dots\cdot{e}^{\frac{{a}_{n}}{\alpha}-1} \\
&={e}^{(\frac{{a}_{1}}{\alpha}-1)+(\frac{{a}_{2}}{\alpha}-1)+\dots+(\frac{{a}_{n}}{\alpha}-1)} \\
&={e}^{\frac{1}{\alpha}\sum\limits_{k=1}^{n}{a}_{k}-n} \\
&={e}^{n-n}\ (\because\ ②) \\
&=1
\end{alignat*}\]
同様に、右辺を、\(k=1\) ~ \(n\) まで掛け合わせると、
\[\begin{alignat*}{3}
右辺&=\prod_{k=1}^{n}\frac{{a}_{k}}{\alpha} \\
&=\frac{1}{{\alpha}^{n}}\prod_{k=1}^{n}{a}_{k}
\end{alignat*}\]
したがって、③より、
\[\begin{alignat*}{3}
&{e}^{\frac{{a}_{k}}{\alpha}-1}\geqq\frac{{a}_{k}}{\alpha} \\
\Leftrightarrow\ &1\geqq\frac{1}{{\alpha}^{n}}\prod_{k=1}^{n}{a}_{k}
\end{alignat*}\]
\[\therefore\ {\alpha}^{n}={\biggl(\frac{1}{n}\sum_{k=1}^{n}{a}_{k}\biggr)}^{n}\geqq\prod_{k=1}^{n}{a}_{k}\]
両辺に \(n\) 乗根をとると、両辺、正の値なので、
\[\frac{1}{n}\sum_{k=1}^{n}{a}_{k}\geqq\sqrt[n]{\prod_{k=1}^{n}{a}_{k}}\]
となり、求める関係が得られました。
また、等号成立は、
\[x=\frac{{a}_{k}}{\alpha}-1=0\ (1\leqq k\leqq n)\]
のときで、整理すると、
\[{a}_{k}=\alpha=\frac{1}{n}\sum_{k=1}^{n}{a}_{k}\]
これは、\(1\leqq k\leqq n\) であるどの \(k\) をとっても、\({a}_{1}\) ~ \({a}_{n}\) の平均と等しい、ということを表しています。
したがって、等号成立は \({a}_{1}=\)\(\ {a}_{2}=\)\(\ \dots=\)\(\ {a}_{n}\) のときであることがわかりました。
(証明終了)
おわりに
お疲れさまでした!今回は、相加平均と相乗平均の関係を見てきました。
こちらの関係式は、それ自体を証明する問題も出題されますが(特に共通テスト)、この関係を使って、別の命題を証明させる問題が比較的多いようです。
ぜひ、証明も合わせて、使いこなせるようになりましょう!
特に、以下の2点は、相加平均と相乗平均の関係を利用する問題で狙われやすいポイントです。ぜひ、ご自身で問題を解かれる際は、毎回意識して確認するようにしましょう。
【相加平均と相乗平均の関係を利用する際に意識するポイント】
- \(x,y>0\)
- 等号成立条件
【相加平均と相乗平均の関係(文字が2つの場合)】
\(x,y>0\) に対して、
\[\frac{x+y}{2}\geqq\sqrt{xy}\]
(等号成立は \(x=y\) のとき)
【(発展)相加平均と相乗平均の関係(文字が3つの場合)】
\(x,y,z>0\) に対して、
\[\frac{x+y+z}{3}\geqq\sqrt[3]{xyz}\]
(等号成立は \(x=y=z\) のとき)
【(発展)相加平均と相乗平均の関係(文字が \(n\) 個の場合)】
正の数の数列 \(\{{a}_{n}\}\) に対して、
\[\frac{1}{n}\sum_{k=1}^{n}{a}_{k}\geqq\sqrt[n]{\prod_{k=1}^{n}{a}_{k}}\]
(等号成立は \({a}_{1}=\)\(\ {a}_{2}=\)\(\ \dots=\)\(\ {a}_{n}\) のとき)
※\(\prod\) は \(\sum\) と同様に、\(k=1\) ~ \(n\) まで、\({a}_{k}\) を掛け算するという記号です



コメント