指数法則（指数が自然数の場合）

解説

\({a}^{m+n}={a}^{m}\cdot{a}^{n}\)

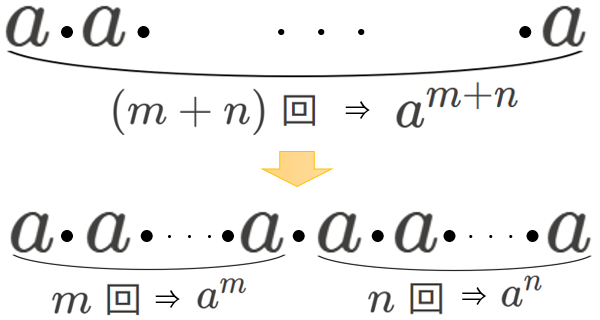
この左辺は、\(a\) が、\((m+n)\) 回掛け算されている、ということと同じ意味です。
そして、これは、

• \(a\) を \(m\) 回掛け算された部分
• \(a\) を \(n\) 回掛け算された部分

とに分けることができます。（下の図参照）

したがって、\({a}^{m+n}={a}^{m}\cdot{a}^{n}\) が導けました。

\({a}^{m-n}={a}^{m}\div{a}^{n}\quad(a\ne 0，m>n)\)

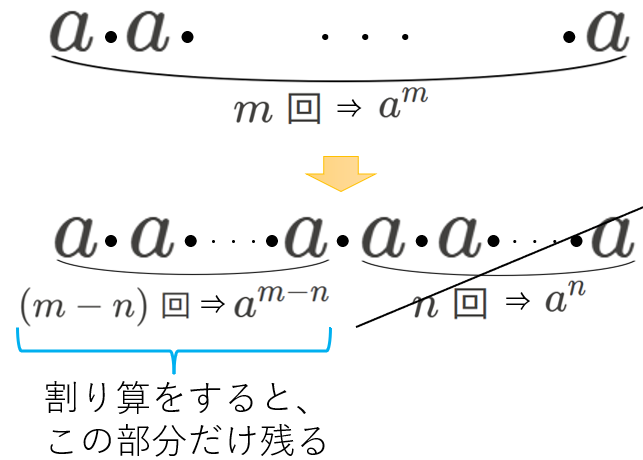
自然数 \(m\) は、\(m=(m-n)+n\) と変形できます。

また、\(m，n\) がいずれも自然数で、かつ、\(m>n\) のとき、\((m-n)\) も自然数になることに注意すると、上の \({a}^{△+■}={a}^{△}\cdot{a}^{■}\) という公式を使えば、以下の式が成り立ちます。（△に \(m-n\)、■に \(n\) を代入しました）

\[{a}^{m}={a}^{m-n}\cdot{a}^{n}\]

ここで、\(a\ne 0\) なので、\({a}^{n}\ne 0\) であることに注意して（\(0\) でない実数を何乗しても、\(0\) にはならない）、両辺を \({a}^{n}\) で割ると、

\[{a}^{m-n}={a}^{m}\div{a}^{n}\]

が得られました。

\(({a}^{m})^{n}={a}^{mn}\)

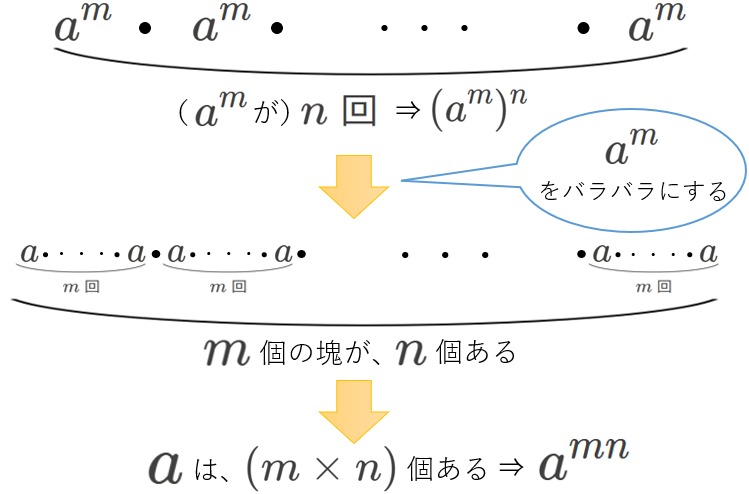
左辺は、\({a}^{m}\) が、\(n\) 回掛け算されている、ということと同じ意味です。

そして、このとき、\(a\) の個数に注目すると、\(a\) は、\((m\times n)\) 回掛け算されていることがわかります。（下の図参照）

したがって、\(({a}^{m})^{n}={a}^{mn}\) が導けました。

\({(ab)}^{m}={a}^{m}\cdot{b}^{m}\)

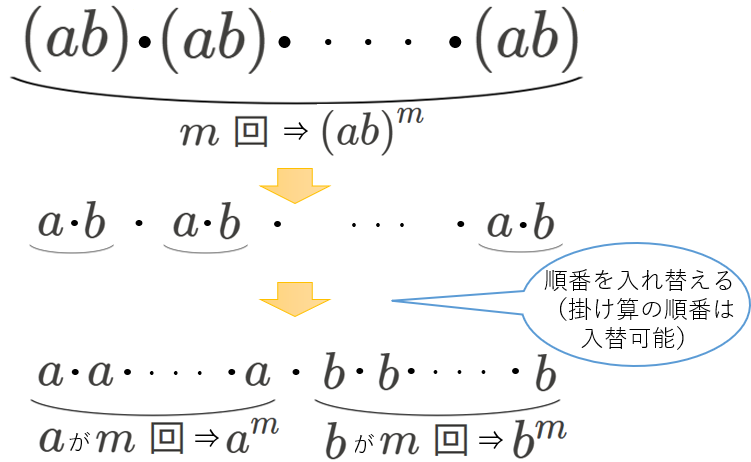
左辺は、\(ab\) が、\(m\) 回掛け算されている、ということと同じ意味です。

そして、掛け算の順番は入替可能なことに注意すると、このとき、\(a\) の個数に注目すると、\(a\) は、\((m\times n)\) 回掛け算されていることがわかります。（下の図参照）

したがって、\({(ab)}^{m}={a}^{m}\cdot{b}^{m}\) が導けました。

\((\frac{a}{b})^{m}=\frac{{a}^{m}}{{b}^{m}}\quad(b\ne 0)\)

上で確認した、\({(ab)}^{m}={a}^{m}\cdot{b}^{m}\) という公式について、\(b\ne 0\) の場合を考えます。

\(b\ne 0\) なので、\({b}^{m}\ne 0\) であることに注意して（\(0\) でない実数を何乗しても、\(0\) にはならない）、両辺を \({b}^{m}\) で割ると、

\[\frac{(ab)^{m}}{{b}^{m}}={a}^{m}\quad・・・①\]

ここで新たな文字 \(a’\) を用意して、以下のように定義します。

\[a’=ab\quad・・・②\]

②の両辺を \(b\ (\ne 0)\) で割ると、

\[a=\frac{a’}{b}\quad・・・③\]

②③を①に代入すると、

\[\frac{{(a’)}^{m}}{{b}^{m}}=\biggr(\frac{a’}{b}\biggr)^{m}\]

この式の \(a’\) を \(a\) と置き直し、左辺と右辺を入れ替えれば、

\[\biggr(\frac{a}{b}\biggr)^{m}=\frac{{a}^{m}}{{b}^{m}}\]

を得られました。

おわりに

今回は、指数が自然数の場合の、指数法則を解説しました。

「指数が自然数の場合の」とつけたのは、実は、この指数法則は、自然数以外（整数・有理数・実数・複素数）の場合にも成り立つためです！（※）
※複素数の場合に、指数法則が成立するためは、いくつか条件を与える必要があります。

複素数を除いた、整数・有理数・実数の場合については、数学IIのほうで解説していますので、興味を持たれた方は確認してみてください！

（※ここからは少々発展的な内容なので、お時間ない方は飛ばしてください）

ちなみに、\({a}^{m-n}={a}^{m}\div{a}^{n}\quad(a\ne 0，m>n)\) の導出を少し思い出してみましょう。（忘れた方は、解説へジャンプ）

こちらの導出は、

自然数の範囲で確認済の \({a}^{△+■}={a}^{△}\cdot{a}^{■}\) という公式を利用する

という方針で進めるために、\(m>n\) という条件を設けました。

この条件が、もし無ければ、

• \(m=n\) のとき、左辺\(={a}^{0}\)，右辺\(={a}^{m}\div{a}^{m}=1\)
• \(m<n\) のとき、\(m-n<0\) のため、左辺は、実数 \(a\) のマイナス乗

という式を得ることができます。これの何がうれしいかというと、

• 今までは、指数には、自然数しか入れることができなかった
• 自然数で得られた性質を、より広い範囲（整数・有理数・実数・複素数）で利用できるようにすることで、より広い範囲で、計算したり、様々な性質を確かめたりできる

ということになります。

大学の数学では、このような「拡張」を考えることが、しばしばあります。ぜひ、興味を持たれた方は調べてみてください。