今回は、組立除法による整式の割り算について解説します。
組立除法は、整式の割り算を行うための一つの方法で、割る式が1次式の場合しか使えないという制限はあるものの、筆算と比べて書く量が少なくて済み、圧倒的に早く計算できます。
共通テストなど、1分1秒を争う試験の場合、組立除法を使いこなせることは、非常に大きなアドバンテージになります。
ぜひ、組立除法をマスターして、計算力を向上させましょう!
解説
組立除法のやり方
それでは、例題を元に、組立除法のやり方を見ていきましょう。
割る式の \(x\) の係数が1の場合
<例題>
整式 \(P(x)=2{x}^4-3{x}^{3}+5{x}^{2}-x+1\) を、\((x-3)\) で割り算せよ
<解法>
① 割られる式の係数と、割る式 \((x-\alpha)\)の \(\alpha\) を、下の図のように並べ、最高次の係数を下ろす
※今回の例では、\((x-3)\) なので、\(\alpha=3\) となります
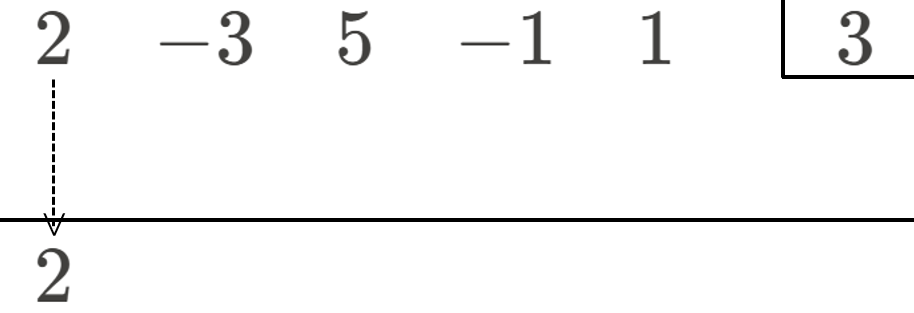
② 下した最高次の係数と、\(\alpha\) を掛け算した結果を、右隣の係数の下に書き足す
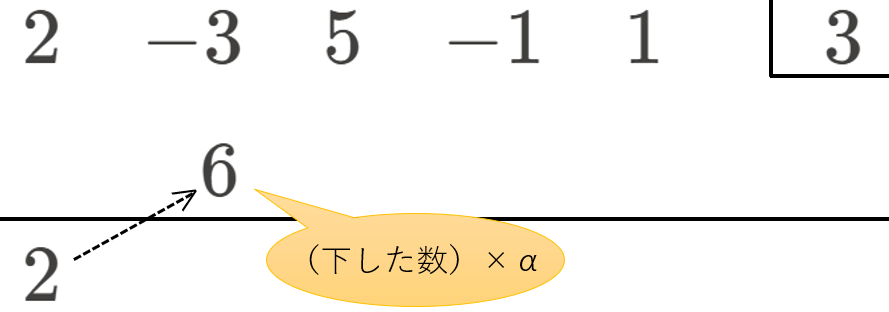
③ 書き足した位を、上から下に足し算し、その結果を下ろす
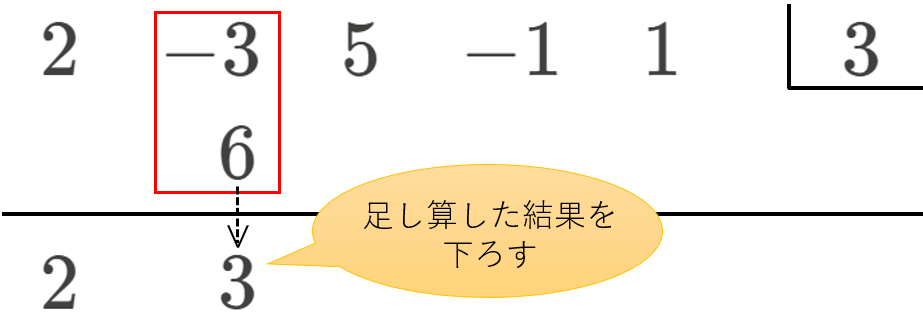
④ ②③を繰り返す
(② \(\alpha\) 倍⇒③足し算⇒② \(\alpha\) 倍⇒③足し算⇒・・・)
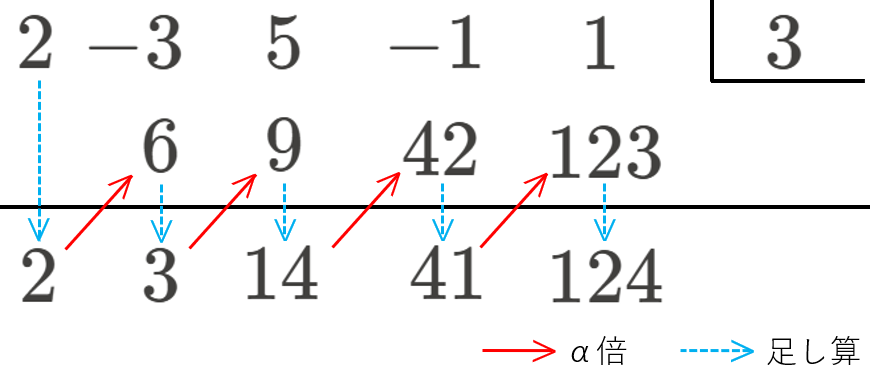
⑤ 最低次の項(定数項)まで繰り返したら、操作は完了。以下のように商と余りが求められる。

割る式の \(x\) の係数が1以外の場合
続いて、割る式の \(x\) の係数が1以外の場合を見てみます。
とはいえ、係数が1の場合とほとんど同じで、ほんの少し操作が増えるだけなので、安心してください!
<例題>
整式 \(P(x)=2{x}^4-3{x}^{3}+5{x}^{2}-x+1\) を、\((2x-3)\) で割り算せよ
<解法>
① 割る式の係数が1になるように、割る式を変形する
今回の例題では、\((2x-3)=2(x-\frac{3}{2})\) と変形します。
② ①の変形で得られた \((x-\alpha)\) を割る式として、割る式の \(x\) の係数が1の場合の組立除法を行う
今回の例題では、\(P(x)\) を \((x-\frac{3}{2})\) で割り算し、
\[P(x)=\Bigl(x-\frac{3}{2}\Bigr)\Bigl(2{x}^{3}+5x+\frac{13}{2}\Bigr)+\frac{43}{4}\]
という結果が得られます。
(ぜひ、練習のためにもご自身でを動かして計算してみてください!)
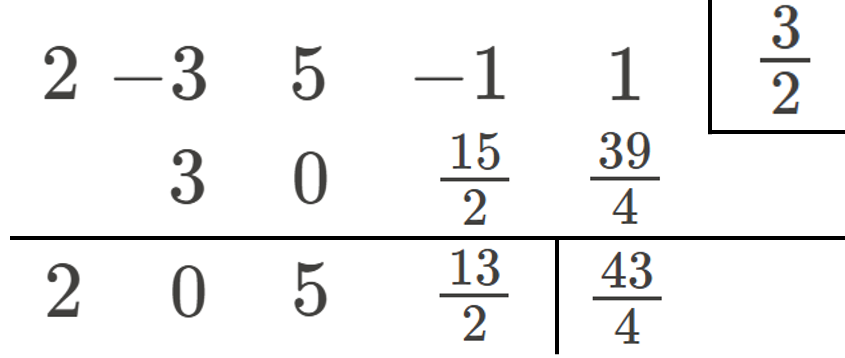
③ ①の変形を元に戻す
\[\begin{alignat*}{3}
P(x)&=\Bigl(x-\frac{3}{2}\Bigr)\Bigl(2{x}^{3}+5x+\frac{13}{2}\Bigr)+\frac{43}{4} \\
&={\small\frac{1}{2}\cdot\Biggl\{2\Bigl(x-\frac{3}{2}\Bigr)\Biggr\}\Bigl(2{x}^{3}+5x+\frac{13}{2}\Bigr)+\frac{43}{4}} \\
&={\small\Biggl\{2\Bigl(x-\frac{3}{2}\Bigr)\Biggr\}\Biggl\{\frac{1}{2}\Bigl(2{x}^{3}+5x+\frac{13}{2}\Bigr)\Biggr\}+\frac{43}{4}} \\
&=(2x-3)\Bigl({x}^{3}+\frac{5}{2}x+\frac{13}{4}\Bigr)+\frac{43}{4}
\end{alignat*}\]
したがって、商 \({x}^{3}+\frac{5}{2}x+\frac{13}{4}\)、余り \(\frac{43}{4}\) と求めることができました。
組立除法で商と余りが求められる理由(原理)
ここまでで、組立除法を利用した整式の割り算の方法を見てきました。
最後に、なぜ組立除法により整式の割り算ができるのか、について見ていきたいと思います。
【組立除法により整式の割り算ができる理由】
<証明>
n次の整式 \(P(x)={a}_{n}\cdot{x}^{n}\)\(+{a}_{n-1}\cdot{x}^{n-1}\)\(+・・・\)\(+{a}_{1}\cdot x\)\(+{a}_{0}\) を \((x-\alpha)\) で割り算することを考えます。
組立除法により得られた結果の数列を \(\{{b}_{n}\}\) とすると、次の図のようになります。
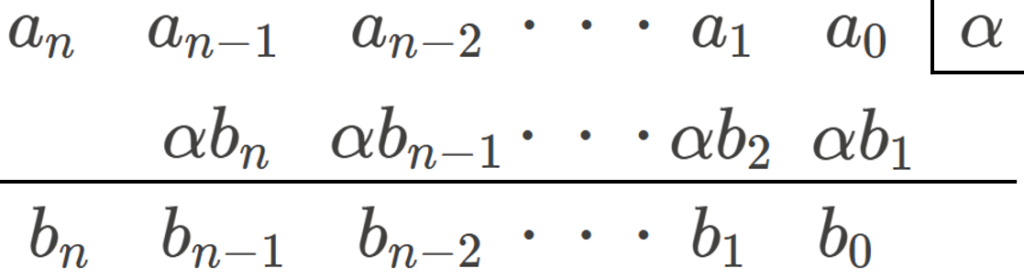
したがって、
\[\begin{alignat*}{3}
{b}_{n}&={a}_{n} \\
{b}_{n-1}&={a}_{n-1}+\alpha{b}_{n} \\
{b}_{n-2}&={a}_{n-2}+\alpha{b}_{n-1} \\
& ・・・ \\
{b}_{1}&={a}_{1}+\alpha{b}_{2} \\
{b}_{0}&={a}_{0}+\alpha{b}_{1}
\end{alignat*}\]
移項して、「\({a}_{k}=\)」の形にすると、
\[\begin{alignat*}{3}
{a}_{n}&={b}_{n} \\
{a}_{n-1}&={b}_{n-1}-\alpha{b}_{n} \\
{a}_{n-2}&={b}_{n-2}-\alpha{b}_{n-1} \\
& ・・・ \\
{a}_{1}&={b}_{1}-\alpha{b}_{2} \\
{a}_{0}&={b}_{0}-\alpha{b}_{1}
\end{alignat*}\]
この結果を、整式 \(P(x)\) の式に戻すと、
\[\begin{alignat*}{3}
P(x)&={a}_{n}\cdot{x}^{n} \\
&\qquad+{a}_{n-1}\cdot{x}^{n-1} \\
&\qquad+{a}_{n-2}\cdot{x}^{n-2} \\
&\qquad+・・・ \\
&\qquad+{a}_{1}\cdot x \\
&\qquad+{a}_{0} \\
&={b}_{n}\cdot{x}^{n} \\
&\qquad+({b}_{n-1}-\alpha{b}_{n})\cdot{x}^{n-1} \\
&\qquad+({b}_{n-2}-\alpha{b}_{n-1})\cdot{x}^{n-2} \\
&\qquad+・・・ \\
&\qquad+({b}_{1}-\alpha{b}_{2})\cdot x \\
&\qquad+({b}_{0}-\alpha{b}_{1}) \\
&=(x-\alpha)\cdot{b}_{n}\cdot {x}^{n-1} \\
&\qquad+(x-\alpha)\cdot{b}_{n-1}\cdot {x}^{n-2} \\
&\qquad+・・・ \\
&\qquad+(x-\alpha)\cdot{b}_{3}\cdot {x}^{2} \\
&\qquad+(x-\alpha)\cdot{b}_{2}\cdot x \\
&\qquad+(x-\alpha)\cdot{b}_{1} \\
&\qquad+{b}_{0} \\
&={\small(x-\alpha)} \\
&{\small\qquad\times({b}_{n}\cdot {x}^{n-1}+・・・+{b}_{2}\cdot x+{b}_{1})} \\
&\qquad\qquad+{b}_{0}
\end{alignat*}\]
したがって、組立除法で得られた各 \({b}_{k}\) は、
- \({b}_{n},{b}_{n-1},・・・,{b}_{1}\):商の係数
- \({b}_{0}\):余り
となることがわかり、組立除法により整式の割り算ができることが示されました。
(証明終了)
おわりに
お疲れさまでした!今回は、組立除法による整式の割り算を見てきました。
組立除法により、機械的に商と余りを求められることが理解いただけたのではないかと思います。
整式の割り算は、「割り算せよ」といったダイレクトに割り算をさせる問題というよりは、問題を解く過程で、整式の割り算が必要になるというケースが多いかと思います。
こんなとき、計算に時間がかかったり、計算方法に不安が残っていると、本来時間をかけて丁寧な検討が必要な部分に割ける時間が少なくなり、手薄な検討になってしまいかねません。
ぜひ、何度も練習問題に当たり、息をするように計算ができるように、しっかりと準備をしておきましょう!



コメント