整式の割り算

解説

整式の割り算とは

自然数の割り算は、小学校の算数で勉強しますが、その定義を小難しく書くと、こんな感じになります。

見た目はかなりイカつい感じになりましたが、言っていることはとてもシンプルで、みなさんがよく知っている、あの割り算です。

（例）
「\(p=15\) を \(a=6\) で割り算する」とは、

• \(15=6\times q+r\)
• \(6>r\)

を満たす \(q，\)\(r\) を求めることです。

そして、\(q=2，\)\(r=3\) とすると、2つの関係を満たします。

• \(15=6\times 2+3\)
• \(6>r=3\)

この「自然数の割り算」の定義（考え方）を、整式でも導入します。
そうすると、「整式の割り算」とは、以下のような定義になります。

どうでしょう。自然数の場合の割り算の定義と、とてもよく似てますよね！

ただ、1つだけ大きく違うところがあり、
それは、2つ目の関係が、「\(A(x)\) の次数 \(>\) \(R(x)\) の次数」となっているところです。

つまり、自然数の場合は、割る式 \((a)\) と 余り \((r)\) をそのまま大小関係を見ていたところ、整式に導入するにあたり、定義が少しだけ修正されますので、要注意です！

自然数の場合と同様、具体例を見てみましょう。

（例）
「\(P(x)={x}^{2}-3x+7\) を \(A(x)=x+2\) で割り算する」とは、

• \({x}^{2}-3x+7=(x+2)\times Q(x)+R(x)\)
• \(((x+2)\) の次数 \((=1))\ >(R(x)\) の次数\()\)

を満たす \(Q(x)，\)\(R(x)\) を求めることです。

そして、\(Q(x)=x-5，\)\(R(x)=17\) とすると、2つの関係を満たします。
（整式の割り算の具体的な方法は、次の章で解説します。）

• \({x}^{2}-3x+7=(x+2)\times(x-5)+17\)
• \(((x+2)\) の次数 \((=1))\ >(R(x)\) の次数 \((=0))\)

整式の割り算のやり方（筆算を用いた方法）

それでは、実際に、整式の割り算のやり方を見ていきましょう。

ここでは筆算を用いた方法を解説します。

※組立除法（1次の場合）、恒等式を作って係数比較など、いくつか方法はあるのですが、個人的には、結局、愚直に筆算するのが一番早く・計算ミスを少なくできる気がしており、ここではこの方法を解説します

（例）
\(2{x}^{4}-5{x}^{3}-6{x}^{2}-15\) を \(2{x}^2-x+3\) で割った余り

割り算の筆算は次のようになり、
\(Q(x)={x}^{2}-2x-\frac{11}{2}，\)\(R(x)=\frac{1}{2}+\frac{3}{2}\) と求められます。

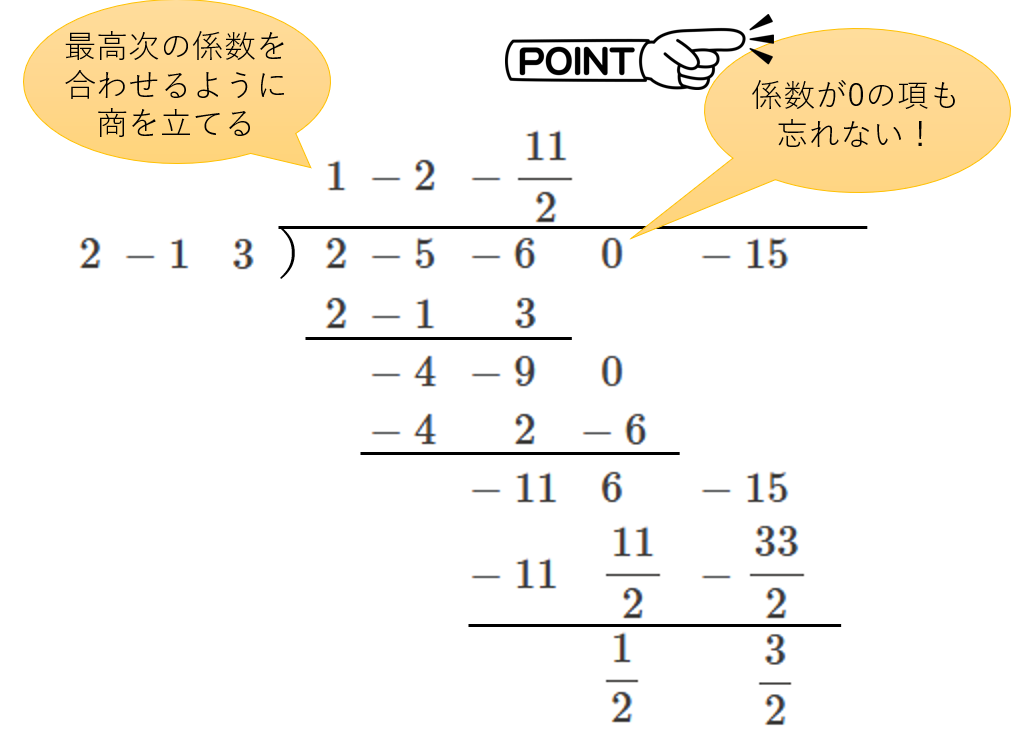
具体的な手順を見てみましょう。

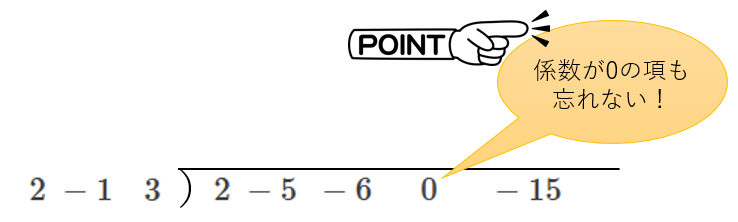
①　割る式・割られる式の係数を並べて書く
まずは、このように、割る式と割られる式の係数を並べて書きます。

、、、と、ここで、最初にして最大のポイントがあります。それは、「係数が \(0\) の項も忘れずに、「\(0\)」と書く」ということです。

今回の例でいえば、割られる式は、\(2{x}^{4}-5{x}^{3}-6{x}^{2}-15\) であり、1次の項がありません。（＝係数が \(0\)）

筆算を書くときは、こちらの1次の項も忘れずに書く必要があります。そうしないと、計算結果が変わってしまいます。

ちなみに、割られる式だけでなく、割る式の場合も、係数が \(0\) の項は忘れずに書くようにしてください。

②　最高次の係数を合わせるように商を立て、引き算
これも、自然数の筆算と同じです。

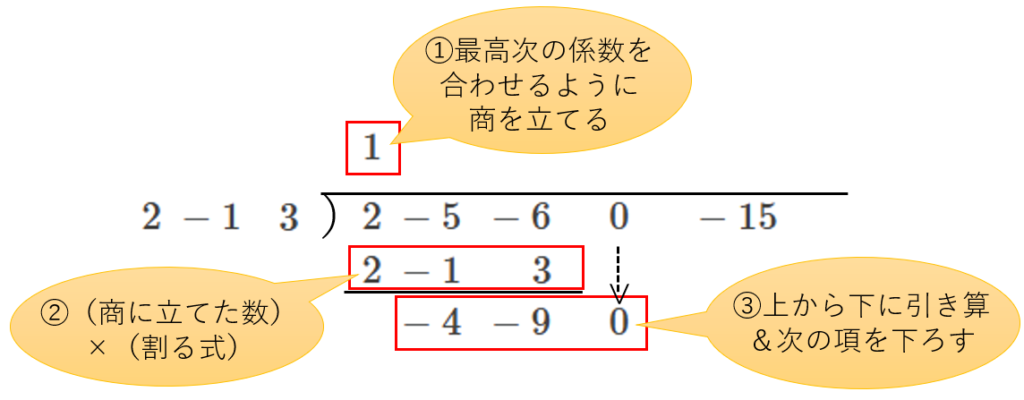
①「割られる式の最高次の係数＝2」「割る式の最高次の係数＝2」なので、商に1を立てる
↓
②低次の項も含めて、商に立てた1を掛け算し、その結果を下に追加
↓
③上から下に引き算し、次の項を下ろす

③　②の操作を繰り返す
②で得られた3つの項に対して、改めて②の操作を行い、一番右まで（下す項が無くなるまで）、これを繰り返します。

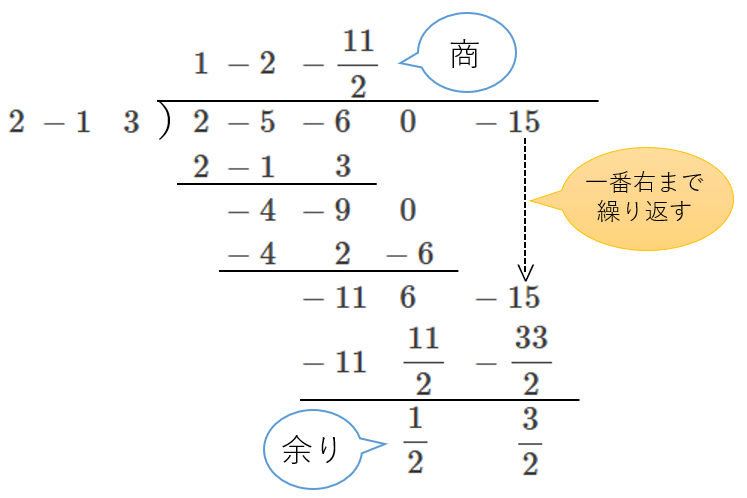
④　③で得られた結果に、\(x\) を戻す
最後に、\(x\) を戻します。

このとき、商と余りの \(x\) の次数が何になるか、が問題になります。
、、、が、そんなに難しくないので、安心してください！ポイントは、割られる式と割る式の最高次の次数です。

商について
今、「割られる式の最高次の次数＝4」「割る式の最高次の次数＝2」でした。

そうすると、（割る式）×（商）の次数＝（割られる式）の次数になるはずなので、商の次数は、2次（＝4-2）となってほしいですよね。

したがって、商の最高次は2次となり、あとは1つずつ次数を減らしていけばOKです。

余りについて
余りはもっと簡単です。

先ほど作成した筆算で、一番右は、定数項でした。
、、、ということは、余りの最低次は自動的に定数項（0次）となり、あとは1つずつ次数を増やしていけばOKです。

お疲れさまでした！以上で、筆算により、整式の割り算ができました！

（発展）整式の割り算の一意性

最後に、整式の割り算の一意性について証明をしてみます。

ここまで当然のように、整式の割り算を、\(P(x)=A(x)\cdot Q(x)+R(x)\) と書き、筆算で具体的な計算をしてきたのですが、実は、これはそんなに当然なことではありません。

どういうことかというと、
筆算で得られた結果は、いくつかある商・余りのペアの1つで、その他にも、商・余りのペアが存在するかもしれません。

もしそうだとすると、それも含めて求めなければ、割り算の結果として十分とは言えません。

、、、が、そのような他の表し方はできず、商・余りのペアはただ1つに決まる、ということが証明できます。ここでは、この証明を見ていきます。

なお、こちらは、少々発展的な内容で、高校数学の範囲を超えている気がするので、お時間がない方は読み飛ばしていただければと思います。

おわりに

お疲れさまでした！今回は、整式の割り算の定義・筆算での計算方法と、割り算の一意性について解説しました。

整式の割り算は、なんとなくわかりにくく、とっつきづらいイメージを持たれている方も多いのではないでしょうか。
その原因は、そもそもの「整式の割り算の定義」自体が、少々わかりにくいことがあると思います。。。

一方で、整式の割り算は、他の分野でも利用することが非常に多く（※）、この整式の割り算ができることを前提に、より発展的な学習をしていくことになります。

ぜひ、以下を繰り返し行い、早めのうちに整式の割り算をマスターしておきましょう！

まずは、慣れ親しんでいる自然数の割り算を、無理やり小難しい言い方に変換してみる
↓
整式バージョンの割り算の定義に挑戦！

※例えば、数学IIIで勉強する以下のような積分では、分数の部分を割り算（赤文字部分）してから、商と余りに分けて計算します。

\[\begin{alignat*}{3}
&\int\frac{\textcolor{#FF0000}{{x}^{3}+60}}{{x}^{2}+5x-1}dx \\
&=\int\frac{\textcolor{#FF0000}{({x}^{2}+5x-1)(x-5)+26x+65}}{{x}^{2}+5x-1}dx \\
&=\int\Bigl\{(x-5)+\frac{13({x}^{2}+5x-1)’}{{x}^{2}+5x-1}\Bigr\}dx \\
&=\frac{1}{2}{x}^{2}-5x+13\log|{x}^{2}+5x-1|+C
\end{alignat*}\]