2点間の距離・点と直線の距離

今回は、2点間の距離・点と直線の距離の公式について、解説します。

公式の導出自体は、三平方の定理が分かればそれほど難しくありませんが、公式を抑えているかどうかで、計算のスピードが大きく変わってきます。
特に、共通テストのような計算力が求められる試験では、これらの公式が威力を発揮します。

一方で、あやふやな知識のままでは、いくらスピードがあったとしても、間違った計算になりかねません。ぜひ、公式の導出を1度は経験し、丸暗記ではない、使える公式の習得を目指しましょう！

それでは解説に入ります。

解説

2点間の距離①（座標を用いた表し方）

まずは、2点間の距離を、座標だけで表す方法を見ていきます。こちらの図をご覧ください。

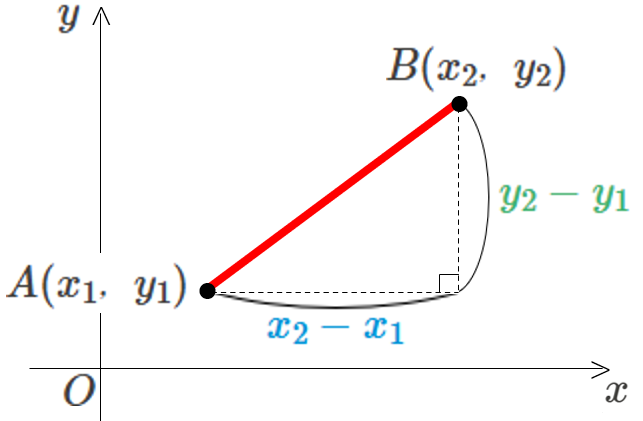
点 \(A，B\) の \(x\) 成分、\(y\) 成分の距離は、それぞれ以下のように表せます。

• \(x\) 成分の距離：\({x}_{2}-{x}_{1}\)
• \(y\) 成分の距離：\({y}_{2}-{y}_{1}\)

したがって、三平方の定理を利用すると、点 \(A，B\) 間の距離は、

\[{AB}^{2}=({x}_{2}-{x}_{1})^{2}+({y}_{2}-{y}_{1})^{2}\]

\(AB\) は距離なので、\(AB>0\) であることに注意すると、

\[AB=\sqrt{({x}_{2}-{x}_{1})^{2}+({y}_{2}-{y}_{1})^{2}}\]

と導くことができました。

2点間の距離②（直線の傾きを用いた表し方）

続いて、直線の傾きと、2点の \(x\) 座標が、\({x}_{1}，{x}_{2}\) と分かっている場合に、使える公式を考えます。
この方法を使えば、2点の \(y\) 座標を具体的に求める必要はありません。

直線の傾きは、

\[\frac{(yの増加量)}{(xの増加量)}\]

という式で表せます。

今、この直線の傾きが \(m\) で、\(x\) の増加量は \({x}_{2}-{x}_{1}\) とわかっているので、

\[\begin{alignat*}{3}
m=\frac{(yの増加量)}{(xの増加量)} \\
=\frac{(yの増加量)}{{x}_{2}-{x}_{1}}
\end{alignat*}\]

\(\therefore\ (yの増加量)=\) \(m({x}_{2}-{x}_{1})\)

これを図示すると、

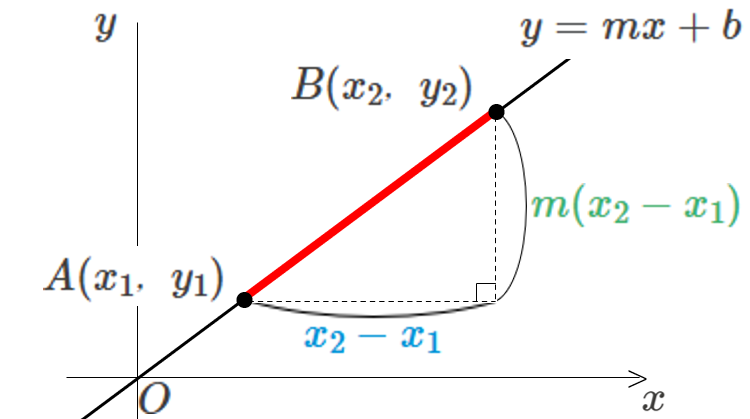
したがって、三平方の定理を利用すると、点 \(A，B\) 間の距離は、

\[\begin{alignat*}{3}
{AB}^{2}&=(xの増加量)^{2}+(yの増加量)^{2} \\
&=({x}_{2}-{x}_{1})^{2}+\{m({x}_{2}-{x}_{1})\}^{2} \\
&=(1+{m}^{2})({x}_{2}-{x}_{1})^{2}
\end{alignat*}\]

\(AB\) は距離なので、\(AB>0\) であることに注意すると、

\[AB=\sqrt{(1+{m}^{2})}\ |{x}_{2}-{x}_{1}|\]

と導くことができました。

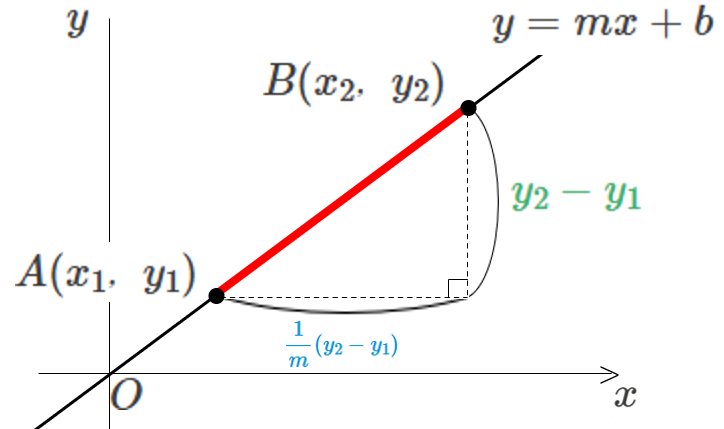
同様に、\(y\) 座標が、\({y}_{1}，{y}_{2}\) と分かっている場合は、

\[(xの増加量)=\frac{1}{m}({y}_{2}-{y}_{1})\]

となることから、

\[\begin{alignat*}{3}
{AB}^{2}&=(xの増加量)^{2}+(yの増加量)^{2} \\
&=\biggr\{\frac{1}{m}({y}_{2}-{y}_{1})\biggr\}^{2}+\{({y}_{2}-{y}_{1})\}^{2} \\
&=(1+{m}^{2})\biggr(\frac{{y}_{2}-{y}_{1}}{m}\biggr)^{2}
\end{alignat*}\]

したがって、

\[AB=\sqrt{1+{m}^{2}}\ \biggr|\frac{{y}_{2}-{y}_{1}}{m}\biggr|\]

となります。

点と直線の距離

次に、座標平面上の点 \(P({x}_{0}，{y}_{0})\) と、直線 \(l：ax+by+c=0\) の間の距離 \(d\) を検討します。

ここでは、まず、\(a\ne 0\) かつ \(b\ne 0\) の場合を考えます。

\(l\) 上に、以下のように、点 \(Q，R，H\) をとると、下の図のようになります。

• \(Q\)：点 \(P\) と \(x\) 座標が等しい、直線 \(l\) 上の点
• \(R\)：点 \(P\) と \(y\) 座標が等しい、直線 \(l\) 上の点
• \(H\)：点 \(P\) から直線 \(l\) に下した垂線の足

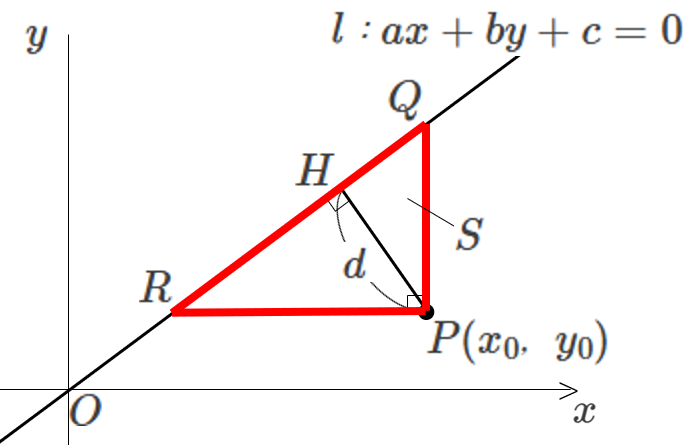
次に、\(\triangle PQR\) の面積 \(S\) を2つの方法で表すことを考えます。

まず、\(PR\) を底辺、\(PQ\) を高さとみると、

\[S=\frac{1}{2}\cdot PR\cdot PQ\quad・・・①\]

また、\(QR\) を底辺、\(PH\) を高さとみると、三平方の定理より、

\[\begin{alignat*}{3}
S&=\frac{1}{2}\cdot QR\cdot PH \\
&=\frac{1}{2}\sqrt{{PQ}^{2}+{PR}^{2}}\cdot d\quad・・・②
\end{alignat*}\]

①＝②より、

\[\frac{1}{2}\cdot PR\cdot PQ=\frac{1}{2}\sqrt{{PQ}^{2}+{PR}^{2}}\cdot d\]

\[\therefore\ d=\frac{PQ\cdot PR}{\sqrt{{PQ}^{2}+{PR}^{2}}}\quad・・・③\]

ここで、\(b\ne 0\)であることに注意すると、点 \(Q\) は直線 \(l\) 上の点なので、点 \(Q\) の \(y\) 座標は、

\[(点Qのy座標)=-\frac{a}{b}{x}_{0}-\frac{c}{b}\]

したがって、

\[\begin{alignat*}{3}
PQ&=|(点Qのy座標)-(点Pのy座標)| \\
&=\biggr|-\frac{a}{b}{x}_{0}-\frac{c}{b}-{y}_{0}\biggr| \\
&=\frac{1}{|b|}|a{x}_{0}+b{y}_{0}+c|\quad・・・④
\end{alignat*}\]

同様に、\(a\ne 0\)であることに注意すると、点 \(R\) は直線 \(l\) 上の点なので、点 \(R\) の \(x\) 座標は、

\[(点Rのx座標)=-\frac{b}{a}{y}_{0}-\frac{c}{a}\]

したがって、

\[\begin{alignat*}{3}
PR&=|(点Rのx座標)-(点Pのx座標)| \\
&=\biggr|-\frac{b}{a}{y}_{0}-\frac{c}{a}-{x}_{0}\biggr| \\
&=\frac{1}{|a|}|a{x}_{0}+b{y}_{0}+c|\quad・・・⑤
\end{alignat*}\]

となり、以下の3式を得られました。

\[\begin{alignat*}{3}
d=\frac{PQ\cdot PR}{\sqrt{{PQ}^{2}+{PR}^{2}}}\quad・・・③ \\
PQ=\frac{1}{|b|}|a{x}_{0}+b{y}_{0}+c|\quad・・・④ \\
PR=\frac{1}{|a|}|a{x}_{0}+b{y}_{0}+c|\quad・・・⑤
\end{alignat*}\]

ここで、④⑤を③に代入すると、

\[\begin{alignat*}{3}
d&=\frac{\frac{1}{|b|}|a{x}_{0}+b{y}_{0}+c|\cdot \frac{1}{|a|}|a{x}_{0}+b{y}_{0}+c|}{\sqrt{\biggr({\frac{1}{|b|}|a{x}_{0}+b{y}_{0}+c|}\biggr)^{2}+\biggr({\frac{1}{|a|}|a{x}_{0}+b{y}_{0}+c|}\biggr)^{2}}} \\
&=\frac{\frac{1}{|ab|}|a{x}_{0}+b{y}_{0}+c|^{2}}{\sqrt{({a}^{2}+{b}^{2})\biggr|\frac{a{x}_{0}+b{y}_{0}+c}{ab}\biggr|^{2}}} \\
&=\frac{\bcancel{\frac{1}{|ab|}}|a{x}_{0}+b{y}_{0}+c|^\bcancel{{2}}}{\bcancel{\frac{|a{x}_{0}+b{y}_{0}+c|}{|ab|}}\sqrt{{a}^{2}+{b}^{2}}} \\
\end{alignat*}\]

となり、

\[d=\frac{|a{x}_{0}+b{y}_{0}+c|}{\sqrt{{a}^{2}+{b}^{2}}}\quad(※)\]

が得られました。

次に、\(b=0\) の場合を考えます。この場合、直線 \(l\) は、

\[x=-\frac{c}{a}\]

の定数関数となり、点 \(P\) との距離 \(d\) は、

\[\begin{alignat*}{3}
d&=\biggr|-\frac{c}{a}-{x}_{0}\biggr| \\
&=\biggr|{x}_{0}+\frac{c}{a}\biggr|
\end{alignat*}\]

一方で、（※）式の右辺に、\(b=0\) を代入すると、

\[\begin{alignat*}{3}
\frac{|a{x}_{0}+c|}{\sqrt{{a}^{2}}}&=\biggr|\frac{a{x}_{0}+c}{a}\biggr| \\
&=\biggr|{x}_{0}+\frac{c}{a}\biggr|=d
\end{alignat*}\]

となり、\(b=0\) の場合も、

\[d=\frac{|a{x}_{0}+b{y}_{0}+c|}{\sqrt{{a}^{2}+{b}^{2}}}\]

を満たします。また、\(a=0\) の場合も同様に計算することで、この式を満たすことがわかります。（ただの計算になるため、ここでは省略）

したがって、\(a=0，b=0\) の場合も含め、

\[d=\frac{|a{x}_{0}+b{y}_{0}+c|}{\sqrt{{a}^{2}+{b}^{2}}}\]

となることがわかりました。

おわりに

今回は、2点間の距離・点と直線の距離の公式を見てきました。

冒頭でも書いた通り、これらの公式は、試験の現場（特に、共通テスト）で、非常に強力な武器になります。
ぜひ、しっかりと覚えて、使える武器を増やしましょう！

また、点と直線の距離の公式については、公式の前提が、
点 \(P({x}_{0}，{y}_{0})\) と、直線 \(l：ax+by+c=0\) の間の距離 \(d\)
となっている点に注意してください。

試験では、\(y=ax+b\) という直線と、ある点との距離を求めさせる問題も、十分に想定されます。

このとき、時間がないからと、そのまま公式を適用するのは、計算ミスの温床となりかなり危険です。
必ず、\(ax+by+c=0\) 型に直線の式を変形した上で、公式を適用するようにしましょう。