微分の公式（\({x}^{n}\) の微分・定数関数の微分）

解説

\({x}^{n}\) の微分

\({x}^{n}\) の微分の公式を、微分の定義から求めていきます。

ちなみに、見た目は非常にシンプルなのですが、公式の導出は意外とハードです。
いきなり挫折してしまうのは非常にもったいないので、よくわからないという方や、共通テスト直前にご覧いただいている方は、次のイメージだけ確実に理解するようにしてください！

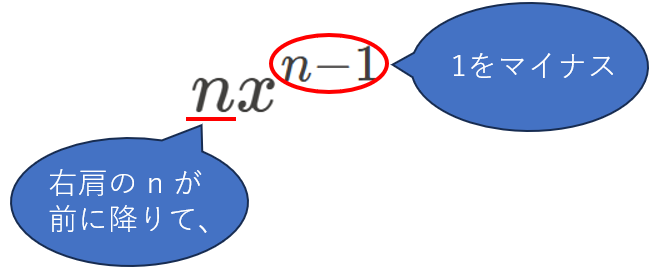
なお、公式の導出自体が試験で出題される可能性もないことはないので、なるべく導出の過程も理解するようにしましょう。

さて、関数 \(f\) の微分の定義は、次の通りです。
\[f'(x)\stackrel{\mathrm{def}}{=} \lim_{h\to 0}\frac{f(x+h)-f(x)}{h}\]

この式に、\(f(x)={x}^{n}\) を代入すると、
\[({x}^{n})’=\lim_{h\to 0}\frac{{(x+h)}^{n}-{x}^{n}}{h}\]
となります。ここで、右辺の分母に着目すると、
\[\begin{alignat*}{3}
&{(x+h)}^{n}-{x}^{n} \\
&=\biggr(\sum^{n}_{k=0}{}_n \mathrm{C}_k\ {x}^{k}{h}^{n-k}\biggr)-{x}^{n}&(※1) \\
&={\small\biggr({x}^{n}+nh{x}^{n-1}+\sum^{n-2}_{k=0}{}_n \mathrm{C}_k\ {x}^{k}{h}^{n-k}\biggr)-{x}^{n}}&\quad(※2) \\
&=nh{x}^{n-1}+\sum^{n-2}_{k=0}{}_n \mathrm{C}_k\ {x}^{k}{h}^{n-k}&(※3)
\end{alignat*}\]

（※1）\({(x+h)}^{n}\) を、二項定理を利用して展開しました。二項定理については、こちらをご覧下さい。

（※2）シグマ \(\sum\) を一部だけ展開し、\(k=n,\ n-1\) の項を外に出しました。

• \(k=n\) の項：\[{}_n \mathrm{C}_n\ {x}^{n}{h}^{n-n}=1\cdot{x}^{n}{h}^{0}={x}^{n}\]
• \(k=n-1\) の項：\[{}_n \mathrm{C}_{n-1}\ {x}^{n-1}{h}^{n-(n-1)}=n{x}^{n-1}{h}^{1}=nh{x}^{n-1}\]

（※3）こちらは、\(n\geqq 2\) の場合の表し方です。\(n=1\) の場合は、シグマ \(\sum\) の項（第2項）が無くなります。

したがって、
\[\begin{alignat*}{3}
&\frac{{(x+h)}^{n}-{x}^{n}}{h} \\
&=\frac{1}{h}\cdot\biggr(nh{x}^{n-1}+\sum^{n-2}_{k=0}{}_n \mathrm{C}_k\ {x}^{k}{h}^{n-k}\biggr) \\
&=\frac{1}{h}\cdot nh{x}^{n-1}+\frac{1}{h}\cdot\sum^{n-2}_{k=0}{}_n \mathrm{C}_k\ {x}^{k}{h}^{n-k} \\
&=n{x}^{n-1}+\sum^{n-2}_{k=0}{}_n \mathrm{C}_k\ {x}^{k}{h}^{n-k-1}
\end{alignat*}\]

ここで、\(n\geqq 2\) の場合、第2項のシグマ \(\sum\) は、以下のように展開でき、どの項にも \(h\) が残っていることがわかります。
\[\begin{alignat*}{3}
\sum^{n-2}_{k=0}&{}_n \mathrm{C}_k\ {x}^{k}{h}^{n-k-1} \\
&={\small{}_n \mathrm{C}_0\ {x}^{0}{h}^{n-1}+{}_n \mathrm{C}_1\ {x}^{1}{h}^{n-2}+} \\
&\qquad・・・ \\
&\qquad{\small+{}_n \mathrm{C}_{n-3}\ {x}^{n-3}{h}^{2}+{}_n \mathrm{C}_{n-2}\ {x}^{n-2}{h}^{1}}
\end{alignat*}\]

そのため、\(h\to 0\) を考えると、このシグマ \(\sum\) は、\(0\) に収束します。

したがって、\(h\to 0\) のとき、
\[\begin{alignat*}{3}
\frac{{(x+h)}^{n}-{x}^{n}}{h}&=n{x}^{n-1}+\sum^{n-2}_{k=0}{}_n \mathrm{C}_k\ {x}^{k}{h}^{n-k-1} \\
&\to n{x}^{n-1}
\end{alignat*}\]
となり、\[({x}^{n})’=n{x}^{n-1}\]が得られました。

定数関数の微分

次に、\(f(x)=c\)（\(c\) は定数）のような形で表される、定数関数 \(f\) の微分を考えます。

こちらも上と同様に、微分の定義式から検討を開始すると、
\[f'(x)\stackrel{\mathrm{def}}{=} \lim_{h\to 0}\frac{f(x+h)-f(x)}{h}\]

ここで、関数 \(f\) は定数関数なので、右辺の分母に現れる \(f(x+h)，f(x)\) は、いずれも \(c\) になります。

そのため、\[\frac{f(x+h)-f(x)}{h}=\frac{c-c}{h}=0\]となり、
\[f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}=\lim_{h\to 0}0=0\]が導出できました。

（発展）\(n\)が自然数でない場合へのの拡張と、拡張を考えることの重要性

ところで、上で求めた、\({x}^{n}\) の微分ですが、右肩の \(n\) は自然数であることを前提に、二項定理を適用して、\(({x}^{n})’=n{x}^{n-1}\) という公式を導出したのでした。

・・・これって、\(n\) が自然数の場合にしか使えないものなのでしょうか？

関数 \(f\) を微分した導関数 \(f’\) を求めることができれば、増減表を書いて、グラフの概形がわかるのでした。
だとすると、自然数から、整数→有理数→実数、と右肩の数字を拡張することができれば、\({x}^{-3}，{x}^{\frac{1}{2}}，{x}^{\sqrt{2}}\) のような関数も、導関数を求めて、グラフを描くことができそうです。

そこで、試しに、自然数から少し飛び出て、\(n=0\) を、\({x}^{n}\) の微分の公式（ \(({x}^{n})’=n{x}^{n-1}\) ）に代入してみましょう。

• 左辺 = \(({x}^{n})’=({x}^{0})’=(1)’=0\quad(※)\)
• 右辺 = \(n{x}^{n-1}=0\cdot{x}^{0-1}=0\)

となり、\({x}^{n}\) の微分の公式は、\(n=0\) の場合も成り立つことがわかりました！
（※）\((1)’=0\) には、上で見た、定数関数の微分の公式を利用しています

今回は、\(n=0\) の場合だけを見ましたが、実は、右肩の数字が、

• 整数でも
• 有理数でも
• 実数でも
• さらには、複素数でも

成立することを確認することができます。（実数までは、数学Ⅲで勉強します）

数学は、以下のような思考プロセスを辿ることが多く、歴代の数学者が、何度もこのプロセスを積み重ねることで、今日まで数学が発展してきました。

今回の \({x}^{n}\) の微分で言えば、

となります。

これは、何も特別なお話ではなく、みなさんも、整数問題や数列の問題で、

• 小さい \(n\) で実験してみる
• 性質がなんとなく掴めたら、因数分解・合同式や、数学的帰納法などのワザを使って、一般的な場合の性質を見つける

ということをされたことがあると思います。

このように、数学の問題を解くにあたり、うれしい性質を、一般的な場合に拡張したい！という思考プロセスは、非常に重要な考え方になります。

ぜひ、考え方・思考プロセスを身に着けてみてください！
（私自身は、この考え方・思考プロセスを身に着けて、数学が理解でしやすくなったと感じています）

おわりに

今回は、\({x}^{n}\) の微分と、定数関数の微分を解説しました。

非常によく使う公式ですが、いざ導出せよ、と言われると、なかなか難しく、手が止まってしまう受験生も多いのではないでしょうか。

これは、1度も経験していないと歯が立たないものである一方で、逆に言えば、1度でも経験しておけば、周りに差をつける大チャンスとも言えます！

ぜひこの機会に、二項定理の復習もかねて、微分の定義から、公式を導出する一連の過程を経験してみましょう！