\[{(x+y)}^{n}=\sum^{n}_{k=0}{}_n \mathrm{C}_k\ {x}^{k}{y}^{n-k}\]
解説
それでは、さっそく導出を始めていきましょう!
・・・と行きたいところなのですが、
式を見ていただくと、シグマ \(\sum\) が入っていたり、\({}_n \mathrm{C}_k\) が入っていたりと、少々ややこしそうに見えてしまいます。
(実際は、そこまでややこしいものではないので、ご安心ください。)
そこで、今回は、以下の流れで導出してみましょう。
- まずは、お試しとして、\(3\) 乗の場合を考えてみる
- \(3\) 乗の場合でなんとなく感覚を掴んでから、\(n\) 乗の場合を考える
\(3\) 乗(\(n=3\))の場合 ※お試し
係数とパターン数の関係
まず、\({(x+y)}^{3}\) を展開すると、以下の式となります。\[{(x+y)}^{3}={x}^{3}+3{x}^{2}y+3x{y}^{2}+{y}^{3}\]
ここからは、この右辺の各項の係数が、どのようにして出てきたのかを考えることにします。
左辺を、あえて、\({(x+y)}^{3}\) ではなく、\((x+y)(x+y)(x+y)\) とバラして考えると、次の図のようになります。
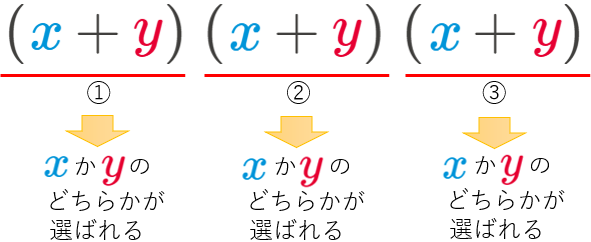
そして、\({x}^{3}\) 乗の項は、①②③で、全て \(x\) が選ばれた場合だけ現れることになります。(パターン数は \(1\))
また、\({x}^{2}y\) の項は、以下の3つのパターンで現れることがわかります。(パターン数は \(3\))
| ① | ② | ③ | |
| パターン1 | \(x\) | \(x\) | \(y\) |
| パターン2 | \(x\) | \(y\) | \(x\) |
| パターン3 | \(y\) | \(x\) | \(x\) |
同様に、\(x{y}^{2}\) の項は、以下の3つのパターンで現れます。(パターン数は \(3\))
| ① | ② | ③ | |
| パターン1 | \(x\) | \(y\) | \(y\) |
| パターン2 | \(y\) | \(x\) | \(y\) |
| パターン3 | \(y\) | \(y\) | \(x\) |
最後に、\({y}^{3}\) 乗の項は、①②③で、全て \(y\) が選ばれた場合だけ現れます。(パターン数は \(1\))
つまり、各項のパターン数をまとめると、以下のようになります。
| \({x}^{3}\) | \({x}^{2}y\) | \(x{y}^{2}\) | \({y}^{3}\) | |
| パターン数 | 1 | 3 | 3 | 1 |
ここで、もう一度、\({(x+y)}^{3}\) を展開した式を見てみると、\[{(x+y)}^{3}={x}^{3}+3{x}^{2}y+3x{y}^{2}+{y}^{3}\]
となり、何かに気づきませんか??
そうです!展開したときの係数と、上のパターン数の表が一致しています!
つまり、各項を作り出す「パターン数」が、そのまま各項の「係数」になる、ということがわかりました。
| \({x}^{3}\) | \({x}^{2}y\) | \(x{y}^{2}\) | \({y}^{3}\) | |
| パターン数 | 1 | 3 | 3 | 1 |
| 各項の係数 | 1 | 3 | 3 | 1 |
各項を作り出す「パターン数」が、そのまま各項の「係数」になる
パターン数(=係数)を \({}_3 \mathrm{C}_○\) の形で表す
では、この「パターン数」を \({}_3 \mathrm{C}_○\) の形で表すことを考えてみましょう。
この検討により、二項定理の \({(x+y)}^{n}=\sum\limits^{n}_{k=0}{}_n \mathrm{C}_k\ {x}^{k}{y}^{n-k}\) という式に近づきます。
もう一度、\({x}^{2}y\) の項を作り出す、3つのパターンを眺めてみましょう。
| ① | ② | ③ | |
| パターン1 | \(x\) | \(x\) | \(y\) |
| パターン2 | \(x\) | \(y\) | \(x\) |
| パターン3 | \(y\) | \(x\) | \(x\) |
\(x\) だけに注目してみると、上の表は、①②③の3つの箱の内、2つを選んで、\(x\) を入れる場合のパターン数と見ることができます。
この、①②③の3つの箱の内、2つを選ぶというのは、\({}_3 \mathrm{C}_2\) の定義そのものです。
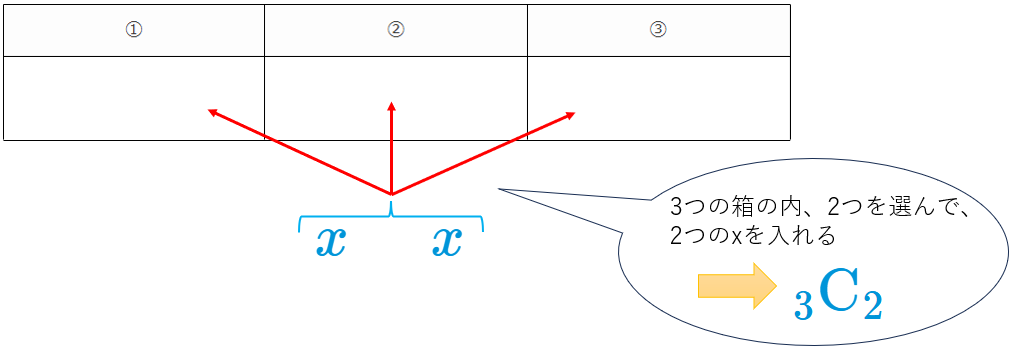
そのため、パターン数(=\({x}^{2}y\) の係数)は、 \({}_3 \mathrm{C}_2\) と表せます。
同様に考えると、
- \({x}^{3}\) のパターン数: \({}_3 \mathrm{C}_3\) \((=1)\)
(①②③の3つの箱の内、3つを選んで、\(x\) を入れた) - \({x}^{2}y\) のパターン数: \({}_3 \mathrm{C}_2\) \((=3)\)
(①②③の3つの箱の内、2つを選んで、\(x\) を入れた) - \(x{y}^{2}\) のパターン数: \({}_3 \mathrm{C}_1\) \((=3)\)
(①②③の3つの箱の内、1つを選んで、\(x\) を入れた) - \({y}^{3}\) のパターン数: \({}_3 \mathrm{C}_0\) \((=1)\)
(①②③の3つの箱の内、0つを選んで、\(x\) を入れた(\(x\) は入れてない))
となります。
よって、\({(x+y)}^{3}\) を展開した式は、\[{\small{(x+y)}^{3}={}_3 \mathrm{C}_3\ {x}^{3}+{}_3 \mathrm{C}_2\ {x}^{2}y+{}_3 \mathrm{C}_1\ {x}{y}^{2}+{}_3 \mathrm{C}_0\ {y}^{3}}\]と表すことができます。
※上で考えた、「パターン数」が、そのまま各項の「係数」になるということを利用しています。
これを、シグマ \(\sum\) を使って一つにまとめると、\[{(x+y)}^{3}=\sum^{3}_{k=0}{}_3 \mathrm{C}_k\ {x}^{k}{y}^{3-k}\]と変形できます。
これで、\(n=3\) の場合の二項定理の式を導くことができました!
\(n\) 乗の場合
それでは、\(n\) 乗の場合を見ていきましょう。
\(n=3\) の場合で見てきたように、「パターン数」が、そのまま各項の「係数」になるのでした。
そして、\({x}^{k}{y}^{n-k}\) の項を考えると、この「パターン数」は、次の図から、\({}_n \mathrm{C}_k\) とわかります。
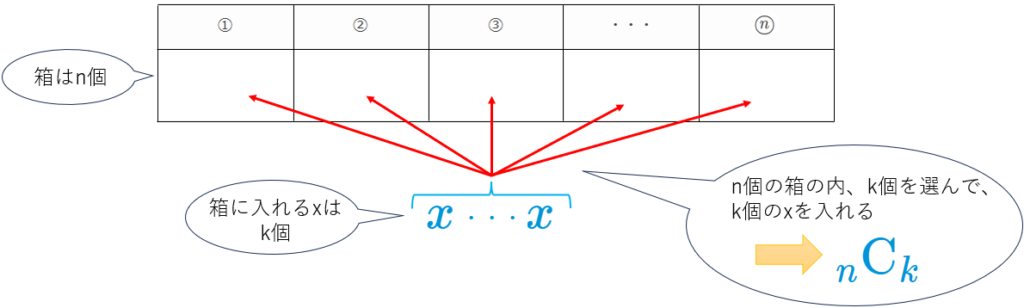
また、\(k\) (=\(x\) の個数)は、\(k=0\) から \(k=n\) まで取りえるので、\[{(x+y)}^{n}=\sum^{n}_{k=0}{}_n \mathrm{C}_k\ {x}^{k}{y}^{n-k}\]これで、二項定理の式が導出できました!お疲れさまでした!
おわりに
今回は、二項定理について解説しました。
導出まで非常に大変だったと思いますが、今回は、とにかく、次の2点がポイントになります。
- 各項を作り出す「パターン数」が、そのまま各項の「係数」になる
- \({x}^{k}{y}^{n-k}\) の項のパターン数は、\({}_n \mathrm{C}_k\)
(\(n\) 個の箱の内、\(k\) 個を選んで \(x\) を入れる)
二項定理の式は、シグマ \(\sum\) や、\({}_n \mathrm{C}_k\) が入っていて少々形が複雑なため、意味を理解しないまま丸暗記するのは、かなり苦しいものがあります。
二項定理に取り組む際は、ぜひ、この2つのポイントを意識してみてください。
\[{(x+y)}^{n}=\sum^{n}_{k=0}{}_n \mathrm{C}_k\ {x}^{k}{y}^{n-k}\]



コメント