等差数列（一般項・和の公式）

解説

等差数列の一般項

初項 \(a\)，公差 \(d\) の等差数列 \(\{{a}_{n}\}\) は、次の図のように表されます。

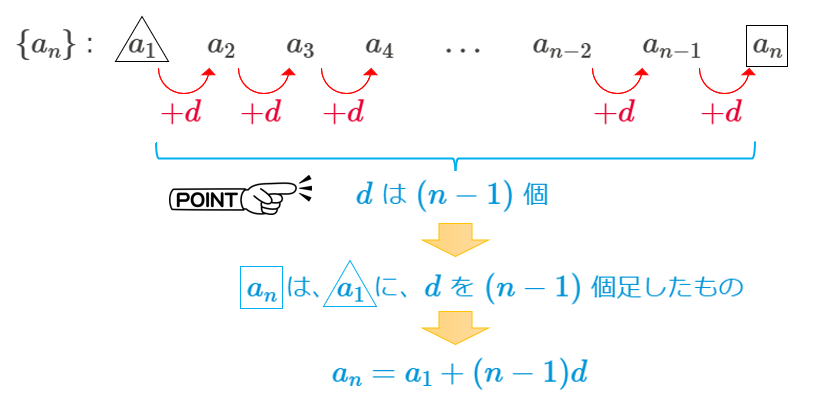
そのため、初項を \(a\) とすると、\[{a}_{n}=a+(n-1)d\]となります。

等差数列の和

初項 \(a\) と末項 \(l\) を用いた表し方

初項 \(a\)，公差 \(d\)，末項 \(l\) の等差数列 \(\{{a}_{n}\}\) について、初項から第 \(n\) 項までの和 \({S}_{n}\) は、次の①②の2通りで表すことができます。

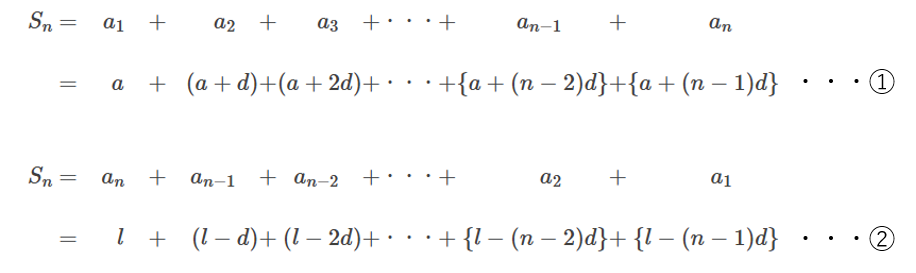
そして、①と②の右辺について、対応する項を上下に足し合わせると、

対応する項の和は、公差 \(d\) に関する部分が消え、全て \((a+l)\) となる

ことがわかります。

また、右辺の項数は \(n\) 個なので、①と②の両辺を足し合わせると、\[2{S}_{n}=(a+l)\times n\]したがって、初項 \(a\)，末項 \(l\) のとき、

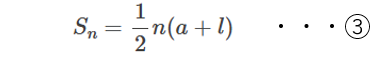
が導出できました。

初項 \(a\) と公差 \(d\) を用いた表し方

次に、この末項 \(l\) を、初項 \(a\) と公差 \(d\) で表すことを考えます。\(l\) は等差数列 \(\{{a}_{n}\}\) の \(n\) 番目の項なので、前半で見た等差数列の一般項の公式より、\[l=a+(n-1)d\]となります。

これを③の式に代入すると、

\[\begin{align}
{S}_{n}&=\frac{1}{2}n[a+\{a+(n-1)d\}] \\
\\
\therefore{S}_{n}&=\frac{1}{2}n\{2a+(n-1)d\}
\end{align}\]

おわりに

今回は、等差数列の一般項と、和の公式を解説しました。

等差数列の公式は、公式の丸暗記ではなく、どのように導出するかを理解すること　がとても重要です。
導出方法を理解できれば、万一、試験中に忘れてしまっても、自分で簡単に導出できますし、そもそも公式も忘れづらくなります。

公式の導出方法について不安な方は、何度も読み返して、ぜひ数列を得点源にしましょう！