連分数展開とその計算

今回は、連分数展開について見ていきます。

高校ではあまり扱われず、高校生の方はそんなに聞き馴染みがないかと思いますが、難関大学の入試で、こちらを背景にした問題がちょくちょく出題されているようです。

考え方ややっていること自体は全然難しくない一方で、「ディオファントス近似」や「超越数」といった、現在でも研究が進められている真っ最中、といった分野とも、密接にかかわるテーマです。

このような研究がしたい方も、そうでない方も、最新の研究の入り口として興味を持っていただける内容になっていますので、ぜひ、気楽な気持ちでご覧いただければうれしいです。

解説

（正則）連分数とは

「連分数展開」について見ていく前に、まず「連分数」とは、そもそも何？ということですが、こういうもののことを言います。

連分数の計算（具体例）

ここまでで連分数・正則連分数の定義を見てきましたが、具体例を見て、よりイメージをつかんでいきましょう。

連分数⇒有理数

まずは、連分数として与えられた値を整理すると何になるかを計算してみましょう。
（こちらは通分を繰り返すだけです）

【例題】
次の連分数を整理せよ。

\[15+\frac{4}{8+\frac{5}{3}}\]

【解答】

\[\begin{alignat*}{3}
15+\frac{4}{8+\frac{5}{3}}=&15+\frac{4}{\frac{24+5}{3}} \\
=&15+\frac{4}{\frac{29}{3}} \\
=&15+\frac{4\times\frac{3}{29}}{\frac{29}{3}\times\frac{3}{29}} \\
=&\frac{435}{29}+\frac{12}{29}=\frac{447}{29}
\end{alignat*}\]

有理数⇒正則連分数（正則連分数展開）

続いて、逆に、有理数を正則連分数に変換したいと思います。

【例題】
\(\frac{64}{11}\) を正則連分数展開せよ

【解答】
有理数の正則連分数展開は、以下の3STEPを繰り返すことで求めていきます。

• ①：「(分子)÷(分母)」で「商」と「余り」を求める　\(\Bigl(\frac{(分子)}{(分母)}=\textcolor{#FF0000}{(商)}+\frac{\textcolor{#00B0F0}{(余り)}}{(分母)}\Bigr)\)
• ②：①の第2項を変形して、\(\frac{1}{\frac{(分母)}{\textcolor{#00B0F0}{(余り)}}}\) の形を作る　\(\Bigl(\frac{(分子)}{(分母)}=\textcolor{#FF0000}{(商)}+\frac{1}{\frac{(分母)}{\textcolor{#00B0F0}{(余り)}}}\Bigr)\)
• ③：①②を、「余り」が \(1\) になるまで繰り返す

それでは、実際にやってみましょう。

＜1セット目＞

• 1-①：\(64\div 11=\textcolor{#FF0000}{5}\) 余り \(\textcolor{#00B0F0}{9}\) なので、\[\frac{64}{11}=\textcolor{#FF0000}{5}+\frac{\textcolor{#00B0F0}{9}}{11}\]
• 1-②：1-①の第2項の(分子)・(分母)に、それぞれ、\(\frac{1}{\textcolor{#00B0F0}{9}}\) を掛け算して、\[\frac{64}{11}=\textcolor{#FF0000}{5}+\frac{\textcolor{#00B0F0}{9}\times\frac{1}{\textcolor{#00B0F0}{9}}}{11\times\frac{1}{\textcolor{#00B0F0}{9}}}=\textcolor{#FF0000}{5}+\frac{1}{\frac{11}{\textcolor{#00B0F0}{9}}}\]

余りは \(\textcolor{#00B0F0}{9}\) で、\(1\) ではなかったため、繰り返します。

＜2セット目＞

• 2-①：\(11\div 9=\textcolor{#FF0000}{1}\) 余り \(\textcolor{#00B0F0}{2}\) なので、\[\frac{11}{9}=\textcolor{#FF0000}{1}+\frac{\textcolor{#00B0F0}{2}}{9}\]
• 2-②：2-①の第2項の(分子)・(分母)に、それぞれ、\(\frac{1}{\textcolor{#00B0F0}{2}}\) を掛け算して、\[\frac{11}{9}=\textcolor{#FF0000}{1}+\frac{\textcolor{#00B0F0}{2}\times\frac{1}{\textcolor{#00B0F0}{2}}}{9\times\frac{1}{\textcolor{#00B0F0}{2}}}=\textcolor{#FF0000}{1}+\frac{1}{\frac{9}{\textcolor{#00B0F0}{2}}}\]

余りは \(\textcolor{#00B0F0}{2}\) で、\(1\) ではなかったため、繰り返します。

＜3セット目＞

• 3-①：\(9\div 2=\textcolor{#FF0000}{4}\) 余り \(\textcolor{#00B0F0}{1}\) なので、\[\frac{9}{2}=\textcolor{#FF0000}{4}+\frac{\textcolor{#00B0F0}{1}}{2}\]

余りが \(\textcolor{#00B0F0}{1}\) となったため、これで操作は終了です。あとは、1～3セットで得られた結果を1つにまとめます。

\[\begin{alignat*}{3}
\frac{64}{11}&=\textcolor{#FF0000}{5}+\frac{1}{\frac{11}{\textcolor{#00B0F0}{9}}}\ (\because\ 1セット目) \\
&=5+\frac{1}{\textcolor{#FF0000}{1}+\frac{1}{\frac{9}{\textcolor{#00B0F0}{2}}}}\ (\because\ 2セット目) \\
&=5+\frac{1}{1+\frac{1}{\textcolor{#FF0000}{4}+\frac{\textcolor{#00B0F0}{1}}{2}}}\ (\because\ 3セット目) \\
&=[5;1,4,2]
\end{alignat*}\]

となり、\(\frac{64}{11}\) を正則連分数で表すことができました！

この求め方のポイントは、STEP②で、

\(\frac{1}{\frac{(分母)}{\textcolor{#00B0F0}{(余り)}}}\) の形を作ること

にあります。

この操作を行うことで、分子は、必ず \(1\) となり、「正則」連分数になる、というわけです。

連分数展開を行う意味

ここまでで、

• 連分数を有理数にする方法
• 有理数を、正則連分数にする方法（正則連分数展開）

を見てきましたが、もうそろそろ、こんな声が聞こえてきそうです。

なんでこんなことしてるの？

おっしゃる通り、これだけだと、何がうれしくてこんな操作をしているのか、良くわからないですよね。。。

そこでこちらの章では、（正則）連分数展開の何がうれしいのか、そのさわりの部分を見ていきたいと思います。

こちらの例をご覧ください。

【例題】
\(\sqrt{3}\) を正則連分数展開せよ。また、その結果を利用して \(\sqrt{3}\) の近似値を求めよ。

【解答】
まず前半部分の正則連分数展開ですが、平方根の場合は、以下の4STEPを繰り返すことで求めていきます。

• ①：与えられた平方根を、整数部分・小数部分に分ける
• ②：小数部分に対して、分子の有理化を行う
• ③：有理化をした小数部分の分子が \(1\) になるように、小数部分を変形する
• ④：小数部分の形に同型が現れるまで繰り返す

それでは、実際にやってみましょう。
なお、連分数展開が少々長くなってしまうので、近似値を求めるところからでいいよー！という方は、こちらをクリックしてください。

＜1セット目＞

• 1-①：「\(1<3<4\ \Longleftrightarrow\ 1<\sqrt{3}<2\)」なので、\(\sqrt{3}\) は、整数部分 \(1，\)小数部分 \((\sqrt{3}-1)\)
• 1-②：1-①で得られた小数部分 \((\sqrt{3}-1)\) に対して、分子の有理化を行うと、\[\begin{alignat*}{3}
  \sqrt{3}&=1+(\sqrt{3}-1) \\
  &=1+\frac{(\sqrt{3}-1)\cdot(\sqrt{3}+1)}{\sqrt{3}+1} \\
  &=1+\frac{2}{\sqrt{3}+1}
  \end{alignat*}\]
• 1-③：1-②で得られた小数部分 \(\frac{2}{\sqrt{3}+1}\) の分子が、\(1\) となるように、(分子)・(分母)に \(\frac{1}{2}\) を掛ける\[\begin{alignat*}{3}\sqrt{3}&=1+\frac{2\times\frac{1}{2}}{(\sqrt{3}+1)\times\frac{1}{2}} \\
  &=1+\frac{1}{\frac{\sqrt{3}+1}{2}}
  \end{alignat*}\]

小数部分の形に同型が現れていないため、繰り返します。

＜2セット目＞

• 2-①：「\(1<\frac{\sqrt{3}+1}{2}<\frac{3}{2}\)」なので、\(\frac{\sqrt{3}+1}{2}\) は、整数部分 \(1，\)小数部分 \(\frac{\sqrt{3}-1}{2}\ \)\((=\frac{\sqrt{3}+1}{2}-1)\)
• 2-②：2-①で得られた小数部分 \(\frac{\sqrt{3}-1}{2}\) に対して、分子の有理化を行うと、\[\begin{alignat*}{3}
  \frac{\sqrt{3}+1}{2}&=1+\frac{\sqrt{3}-1}{2} \\
  &=1+\frac{(\sqrt{3}-1)\cdot(\sqrt{3}+1)}{2\cdot(\sqrt{3}+1)} \\
  &=1+\frac{1}{\sqrt{3}+1}
  \end{alignat*}\]
• 2-③：2-②で得られた小数部分 \(\frac{1}{\sqrt{3}+1}\) の分子は、\(1\) なので、このままでOK

小数部分の形に同型が現れていないため、繰り返します。

＜3セット目＞

• 3-①：「\(2<\sqrt{3}+1<3\)」なので、\(\sqrt{3}+1\) は、整数部分 \(2，\)小数部分 \(\sqrt{3}-1\ \)\((=(\sqrt{3}+1)-2)\)
• 3-②：3-①で得られた小数部分 \(\sqrt{3}-1\) に対して、分子の有理化を行うと、\[\sqrt{3}+1=2+\frac{2}{\sqrt{3}+1}\]
• 3-③：3-②で得られた小数部分 \(\frac{2}{\sqrt{3}+1}\) の分子が、\(1\) となるように、(分子)・(分母)に \(\frac{1}{2}\) を掛ける\[\sqrt{3}+1=2\textcolor{#FF0000}{+\frac{1}{\frac{\sqrt{3}+1}{2}}}\]

ここで、＜1セット目＞の形を思い出すと、

\[\sqrt{3}=1\textcolor{#FF0000}{+\frac{1}{\frac{\sqrt{3}+1}{2}}}\]

であり、小数部分に、全くの同型が現れていることがわかります。そのため、操作はここまででOKです。

ひとまず、1～3セットで得られた結果を1つにまとめてみましょう。

\[\begin{alignat*}{3}
\sqrt{3}&=1+\frac{1}{\frac{\sqrt{3}+1}{2}}\ (\because\ 1セット目) \\
&=1+\frac{1}{1+\frac{1}{\sqrt{3}+1}}\ (\because\ 2セット目) \\
&=1+\frac{1}{1+\frac{1}{2+\frac{1}{\frac{\sqrt{3}+1}{2}}}}\ (\because\ 3セット目)
\end{alignat*}\]

ここで、最後の結果には、小数部分に、全くの同型が現れているので、2セット目で検討した結果を使えます。実際に使ってみると、

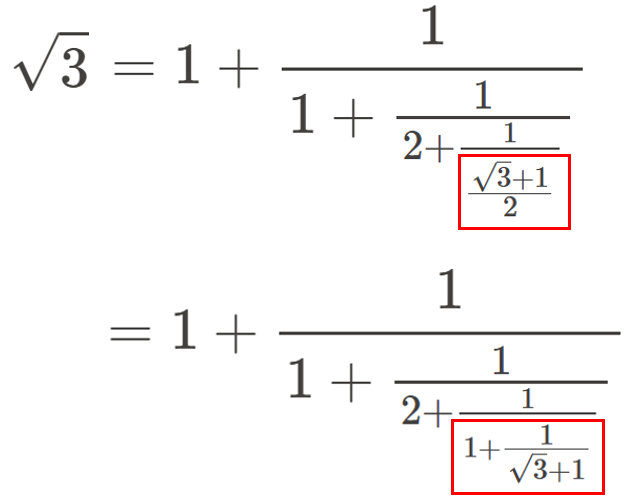
また、この赤枠で囲った形は、2セット目を適用した結果と同型です。

そのため、これを繰り返すと、

\[\sqrt{3}=[1;1,2,1,2,\dots]\]

と求められました。

ここまでで、\(\sqrt{3}\) の正則連分数展開が完了しました。続いて、後半部分の、\(\sqrt{3}\) の近似値を求めていきましょう。

その方法は、以下の通りです。

• 先ほど得られた正則連分数展開の結果を、どこかでぶった切る
• 連分数⇒有理数の変換をおこなう

ここでは試しに5セットまで繰り返した、こちらの結果を利用してみましょう。

\[\sqrt{3}=1+\frac{1}{1+\frac{1}{2+\frac{1}{1+\frac{1}{2+\frac{1}{\frac{\sqrt{3}+1}{2}}}}}}\]

\(1<\frac{\sqrt{3}+1}{2}<\frac{3}{2}\) なので、とりあえず、\(1\) と \(\frac{3}{2}\) の平均 \(\frac{5}{4}\ \)\((=(1+\frac{3}{2})\cdot 2)\) を用いて、\(\frac{\sqrt{3}+1}{2}\risingdotseq\frac{5}{4}\) として、右辺を計算してみると、

\[\begin{alignat*}{3}
&1+\frac{1}{1+\frac{1}{2+\frac{1}{1+\frac{1}{2+\frac{1}{\frac{5}{4}}}}}} \\
&=1+\frac{1}{1+\frac{1}{2+\frac{1}{1+\frac{1}{\frac{14}{5}}}}} \\
&=1+\frac{1}{1+\frac{1}{2+\frac{1}{\frac{19}{14}}}} \\
&=1+\frac{1}{1+\frac{1}{\frac{52}{19}}} \\
&=1+\frac{1}{\frac{71}{52}} \\
&=1+\frac{52}{71} \\
\end{alignat*}\]

この値を計算してみると、\(\textcolor{#FF0000}{1.732}3943\dots\) となり、

\[\sqrt{3}=\textcolor{#FF0000}{1.732}05080757\dots\]

と、小数3桁までは一致しており、それなりに近似できていそうでした。

階層が深くなればなるほど、当然、その精度は上がってきます。

もし興味がある方がいらっしゃれば、ぜひ試してみてください！

おわりに

お疲れさまでした！今回は、連分数展開とその計算方法を見てきました。

実は、正則連分数展開において、平方根の場合は、どこかで必ず周期性が現れる、という非常にありがたい性質があることが知られています。
（厳密には、2次方程式で得られる無理数であり、例えば、黄金比 \(\frac{1+\sqrt{5}}{2}\) 等を含みます）

そのため、平方根であれば、今回のような方法で、必ず近似値を求めることが可能です。

一方で、その他の無理数（例えば、\(e\) とか \(\pi\) とか）については、なかなかそのようなありがたい性質はないものの、

（正則）連分数展開の手法を使えば、これらの無理数も、有理数でそれなりに高い精度で近似できそう！

ということで、研究が進められています。（「ディオファントス近似」や「超越数」などで調べると出てくると思います）

これらの研究は、今まさに研究が進んでいる途中なので、新たな発見をして後世に名前を残したい！！！という、野心にあふれる方は、ぜひ1度調べてみてください！