自然数 \(m,n\ (m\ne 1)\) に対して、既約分数 \(\frac{n}{m}\) を考えたとき、次の2つは同値となる。
- \(\frac{n}{m}\) が、有限小数である
- \(\frac{n}{m}\) の分母の素因数が、2と5のみからなる
今回は、既約分数が有限小数となるための条件について見ていきます。
実は、上の枠内でも見たように、ある既約分数が有限小数になるのは、分母に2と5しか含まれないときだけです。
例えば、\(\frac{1}{3}\) の分母には \(3\) が含まれているし、\(\frac{45}{28}\) の分母には \(7\) が含まれている \((28=7\cdot 4)\) ため、いずれも有限小数にはなりません。
逆に、\(\frac{1}{125}\) の分母には \(5\) しか含まれていない \((125={5}^{3})\) し、\(\frac{n!}{{2}^{1兆}\cdot{5}^{3京}}\) の分母には \(2\) と \(5\) しか含まれていないので、いずれも有限小数になります。
この事実、証明を見れば明らかなのですが、初めて見ると結構ビックリしませんか??
(私は、とてもビックリΣ( ̄□ ̄|||)でした)
今回は、この「ビックリΣ( ̄□ ̄|||)」を共有したくて、こちらの記事を書きました。
丁寧に証明をしていますので、証明の勉強もかねて、気楽に読んでいただけるとうれしいです!
解説
(復習)実数の分類
まずは証明に入る前に、有限小数が実数の中のどこに位置付けられるかを見てみましょう。
(これがわからないと、そもそも何を証明したらいいかも、”???”となってしまうので。。)
| 実数 | 有理数 \(\frac{(整数)}{(整数)}\) の形で書ける実数 | 整数 小数点以下がない有理数 (例:\(3\),\({-123456789}\)) |
| 有限小数 小数点以下が、有限の位までで終わる有理数 (例:\(\frac{5}{8}=0.625\),\({-\frac{54321}{125}}=-434.568\)) | ||
| 循環小数 小数点以下が、周期性を持って、無限に続く有理数 (例:\(\frac{7}{11}=0.636363\dots=0.\dot{6}\dot{3}\)) | ||
| 無理数 ・有理数以外の実数 ・小数点以下が、周期性を持たずに、無限に続く (例:\(\sqrt{2}=1.41421356\dots\ ,\)\(\sqrt{3}=1.73205080\dots\)) | ||
このうち、次の章からは、【「有限小数」になるか/「循環小数」になるか】、について、証明をしていきます。
「既約分数が有限小数となるための条件」の証明
自然数 \(m,n\ (m\ne 1)\) に対して、既約分数 \(\frac{n}{m}\) を考えたとき、次の2つは同値となる。
- \(\frac{n}{m}\) が、有限小数である
- \(\frac{n}{m}\) の分母の素因数が、2と5のみからなる
ここからは、こちらの命題を証明していきます。
これらは、同値のため、\(\Leftarrow,\Rightarrow\) の両方を示す必要があります。
それでは、早速見ていきましょう。
「有限小数である」 \(\Leftarrow\)「分母の素因数が、2と5のみからなる」
<証明>
与えられた条件から、\(0\) 以上の整数 \(k,l\) を用いて、\(m={2}^{k}\cdot{5}^{l}\) と書けます。
(整数 \(k,l\) が同時に \(0\) になると、既約分数 \(\frac{n}{m}\) が整数になってしまうため、その場合は除きます)
したがって、既約分数 \(\frac{n}{m}\) は、
\[\frac{n}{m}=\frac{n}{{2}^{k}\cdot{5}^{l}}\]
となります。この右辺の分母・分子に、\({2}^{l}\cdot{5}^{k}\) を掛け算すると、
\[\begin{alignat*}{3}
\frac{n}{m}&=\frac{n\times({2}^{l}\cdot{5}^{k})}{{2}^{k}\cdot{5}^{l}\times({2}^{l}\cdot{5}^{k})} \\
&\stackrel{\mathrm{(※1)}}{=}\frac{n\times({2}^{l}\cdot{5}^{k})}{{10}^{k+l}}
\end{alignat*}\]
となります。
ここで、\(k,l\) は \(0\) 以上の整数のため、\((k+l)\) も 整数であり、有限の値となります。
したがって、既約分数 \(\frac{n}{m}\) の小数点以下は、有限の位までで終わる(※2)ことがわかり、\(\frac{n}{m}\) は有限小数であることが示されました。
(証明終了)
(※1)こちらの式変形では、指数法則を利用しています。指数法則については、こちらのページをご覧ください。
(※2)整数 \(M,N\) に対し、\(\frac{N}{{10}^{M}}\) を考えると、
分母 \({10}^{\textcolor{#FF0000}{M}}\) は、分子 \(N\) の小数点を、左に \(\textcolor{#FF0000}{M}\) 個移動させます。
この \(M\) が、今、\((k+l)\) で有限の値なので、小数点以下は、有限の位までで終わります。
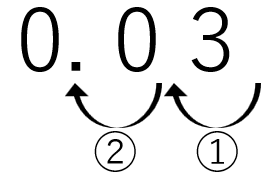
(例)\(0.03=\frac{3}{100}=\frac{3}{{10}^{2}}\) で、分母 \({10}^{\textcolor{#FF0000}{2}}\) は、分子 \(3\) の小数点を、左に \(\textcolor{#FF0000}{2}\) 個移動させる
「有限小数である」 \(\Rightarrow\)「分母の素因数が、2と5のみからなる」
次に、逆向きの矢印を証明します。
<証明>
与えられた条件から、既約分数 \(\frac{n}{m}\) は、有限小数なので、小数点以下の桁数を \(k\) 桁とします。
このとき、\(\frac{n\cdot{10}^{k}}{m}\) は、整数となります。(こちらの理由は、上の(※2)を参照してください)
この値を、整数 \(p\) と置くと、
\[p=\frac{n\cdot{10}^{k}}{m}\]
となり、両辺に \(m\) をかけると、
\[mp=n\cdot{10}^{k}\]
今、\(\frac{n}{m}\) は既約分数であり、\(m,\)\(n\) は互いに素なので、\(m\) は \({10}^{k}={2}^{k}\cdot{5}^{k}\) の約数であることがわかります。(ここでも指数法則を利用しています)
したがって、既約分数 \(\frac{n}{m}\) の分母 \(m\) の素因数は、2と5のみからなることが示されました。
(証明終了)
お疲れさまでした!これにて、次の2つが同値であることが示されました。
- \(\frac{n}{m}\) が、有限小数である
- \(\frac{n}{m}\) の分母の素因数が、2と5のみからなる
おわりに
今回は、既約分数が有限小数となるための条件について見ていきました。
証明を見ていただければ、「確かにそうだよねー」と納得いただけたのではないかと思います。
2つ目の【「有限小数である」 \(\Rightarrow\)「分母の素因数が、2と5のみからなる」】という証明では、「\(m,\)\(n\) は互いに素」ということを用いる、整数問題の定番パターンが現れました。
ぜひ、証明を復習していただき、自分の力で証明できるように練習しておきましょう!
自然数 \(m,n\ (m\ne 1)\) に対して、既約分数 \(\frac{n}{m}\) を考えたとき、次の2つは同値となる。
- \(\frac{n}{m}\) が、有限小数である
- \(\frac{n}{m}\) の分母の素因数が、2と5のみからなる



コメント