【\(\cos\) の加法定理】
一般角 \(\alpha,\beta\) に対し、
\[\cos(\alpha\pm\beta)=\cos\alpha\cos\beta\mp\sin\alpha\sin\beta\]
【\(\sin\) の加法定理】
一般角 \(\alpha,\beta\) に対し、
\[\sin(\alpha\pm\beta)=\sin\alpha\cos\beta\pm\cos\alpha\sin\beta\]
【\(\tan\) の加法定理】
一般角 \(\alpha,\beta\) に対し、
\[\tan(\alpha\pm\beta)=\frac{\tan\alpha\pm\tan\beta}{1\mp\tan\alpha\tan\beta}\]
今回は、加法定理を解説していきます。
こちらの定理は、利用する機会が非常に多く、「咲いたコスモス・コスモス咲いた」なんていうゴロと合わせて覚えている方もいらっしゃるのではないでしょうか。
一方で、この定理がなぜ成立するのか、と聞かれると、困ってしまう方も多いかもしれません。実際に、1999年に、東京大学の数学の入試問題で、\(\sin,\cos\) の加法定理を証明させる問題が出題されたのですが、その当時の正答率はそれほど良くなかったと言われています。。。
国内最高の頭脳を持った受験生が苦戦した問題、と聞くと、戦々恐々としてしまいますが、実はそれほど難しいものではありません。
要は、一度でも導出した経験があるか、ということがポイントになってきます。
今回の解説を通して、「ゴロの暗記でなんとか覚える加法定理」から、「なぜ成立するのか自信をもって答えられる加法定理」にステップアップしていきましょう!
解説
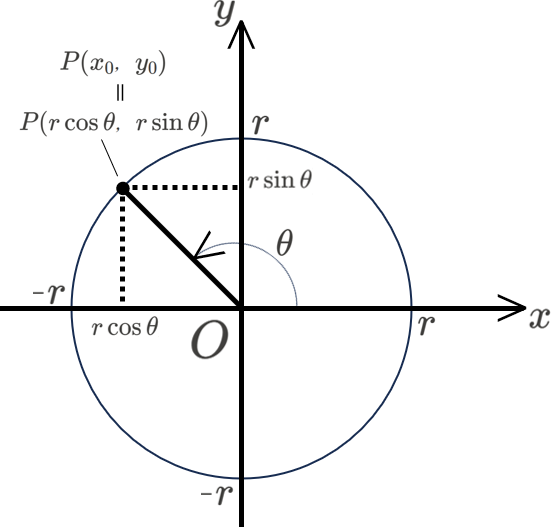
(復習)座標平面を利用した \(\sin,\cos\) の定義
今回は、数学Iで学習した、座標平面を利用した \(\sin,\cos\) の定義を元に解説します。
まだ学習が済んでいない方や、不安があるという方は、先にこちらのページをご覧いただくことをおススメします。
【三角比の \(\theta\geqq90°\) への拡張】
\(xy\) 座標平面に、中心が原点 \(O\)、半径 \(r\) の円をとり、この円周上の点を点 \(P({x}_{0},{y}_{0})\) とする。線分 \(PO\) と\(x\) 軸正の方向とのなす角を \(\theta\) とするとき、\(\sin\theta,\cos\theta,\tan\theta\) を、以下のように定義する。
\[\sin\theta=\frac{{y}_{0}}{r},\cos\theta=\frac{{x}_{0}}{r},\tan\theta=\frac{{y}_{0}}{{x}_{0}}\]
※特に、半径 \(1\) の円(単位円)の場合、
\[\sin\theta={y}_{0},\cos\theta={x}_{0},\tan\theta=\frac{{y}_{0}}{{x}_{0}}\]
\(\cos\) の加法定理
それでは早速、\(\cos\) の加法定理から見ていきます。
以下の図のように、\(xy\) 座標平面上に、単位円と、点 \(A(1,0),\)\(P(\cos\alpha,\sin\alpha),\)\(Q(\cos(\alpha+\beta),\sin(\alpha+\beta))\) をとります。
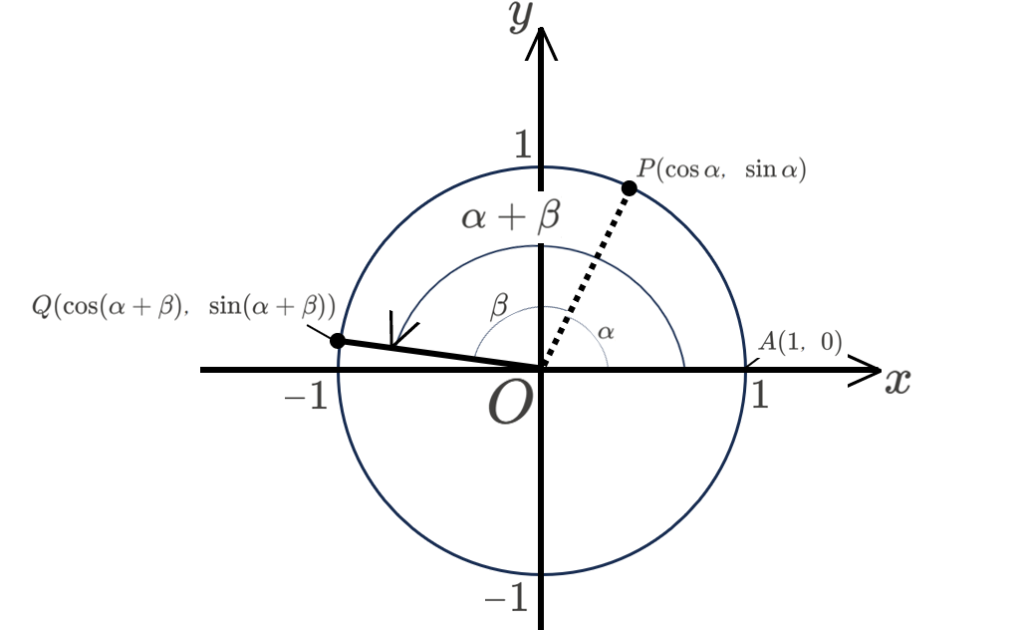
ここで、\((\)線分 \(AQ\) の長さ\()^{2}\) を求めると、
\[\begin{alignat*}{3}
&{AQ}^{2} \\
&={(Q_{x}-A_{x})}^{2}+{(Q_{y}-A_{y})}^{2} \\
&={\{\cos(\alpha+\beta)-1\}}^{2}+{\{\sin(\alpha+\beta)-0\}}^{2} \\
&=\{\cos^{2}(\alpha+\beta)+\sin^{2}(\alpha+\beta)\}-2\cos(\alpha+\beta)+1 \\
&=2-2\cos(\alpha+\beta)\quad・・・①
\end{alignat*}\]
※点 \(A,Q\) の座標を、それぞれ、\(A(A_{x},A_{y}),\)\(Q(Q_{x},Q_{y})\) と表しています。
※2点間の距離については、こちらのページを参照してください。
次に、点 \(A,P,Q\) を 原点中心に \(-\alpha\) 回転させた図形を考え、それぞれ点 \(A'(\cos(-\alpha),\sin(-\alpha)),\)\(P'(1,0),\)\(Q'(\cos\beta,\sin\beta)\) とします。
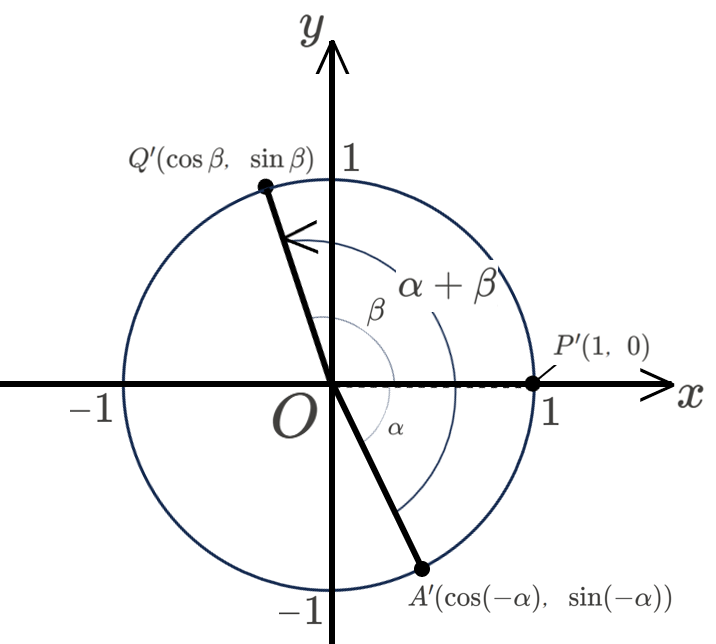
ここで、\((\)線分 \(A’Q’\) の長さ\()^{2}\) を求めると、
\[\begin{alignat*}{3}
&{A’Q’}^{2} \\
&={(Q’_{x}-A’_{x})}^{2}+{(Q’_{y}-A’_{y})}^{2} \\
&={\{\cos\beta-\cos(-\alpha)\}}^{2}+{\{\sin\beta-\sin(-\alpha)\}}^{2} \\
&=\{\cos^{2}(-\alpha)+\sin^{2}(-\alpha)\}+\{\cos^{2}\beta+\sin^{2}\beta\} \\
&\qquad -2\cos(-\alpha)\cos\beta-2\sin(-\alpha)\sin\beta \\
&=2-2(\cos\alpha\cos\beta-\sin\alpha\sin\beta)\quad・・・②
\end{alignat*}\]
※式変形の中で、\(\cos(-\alpha)=\cos\alpha,\)\(\sin(-\alpha)=-\sin\alpha\) という関係を利用しています。
ここで、点 \(A’Q’\) は、点 \(AQ\) を原点中心に \(-\alpha\) 回転させた点なので、\(AQ=A’Q’\) となります。したがって、①=②より、
\[\begin{alignat*}{3}
&{AQ}^{2}={A’Q’}^{2} \\
\Leftrightarrow\ &2-2\cos(\alpha+\beta)= \\
&\qquad\qquad 2-2(\cos\alpha\cos\beta-\sin\alpha\sin\beta) \\
\Leftrightarrow\ &\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta
\end{alignat*}\]
となり、\(\cos(\alpha+\beta)\) の加法定理が得られました。
また、この式において、\(\beta=-\beta’\) とおくと、
\[\begin{alignat*}{3}
&\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta \\
\Leftrightarrow\ &\cos(\alpha-\beta’)=\cos\alpha\cos(-\beta’)-\sin\alpha\sin(-\beta’) \\
\Leftrightarrow\ &\cos(\alpha-\beta’)=\cos\alpha\cos\beta’+\sin\alpha\sin\beta’ \\
&(\because\ \cos(-\beta’)=\cos\beta’,\sin(-\beta’)=-\sin\beta’)
\end{alignat*}\]
\(\beta’\) を、改めて、\(\beta\) とおきなおすと、
\[\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta\]
となり、\(\cos(\alpha-\beta)\) の加法定理が得られました!
\(\sin\) の加法定理
続いて、\(\sin\) の加法定理を見ていきます。
こちらは、以下の3つの関係から、式変形により導出していきます。
- ① \(\cos\) の加法定理
- ② \(\cos(\frac{\pi}{2}-\theta)=\sin\theta\)
- ③ \(\sin(\frac{\pi}{2}-\theta)=\cos\theta\)
まず、②の関係より、
\[\cos\Bigl\{\frac{\pi}{2}-(\alpha\pm\beta)\Bigr\}=\sin(\alpha\pm\beta)\quad(※)\]
となります。
この左辺を、\(\cos\{(\frac{\pi}{2}-\alpha)\mp\beta\}\) と考えて、式変形すると、
\[\begin{alignat*}{3}
&\cos\Bigl\{\frac{\pi}{2}-(\alpha\pm\beta)\Bigr\} \\
&=\cos\Biggl\{\Bigl(\frac{\pi}{2}-\alpha\Bigr)\mp\beta\Biggr\} \\
&=\cos\Bigl(\frac{\pi}{2}-\alpha\Bigr)\cos\beta\pm\sin\Bigl(\frac{\pi}{2}-\alpha\Bigr)\sin\beta \\
&\quad(\because\ ①\ \cos\ の加法定理) \\
&=\sin\alpha\cos\beta\pm\cos\alpha\sin\beta \\
&\quad(\because\ ②③の関係式)
\end{alignat*}\]
したがって、(※)より、
\[\sin(\alpha\pm\beta)=\sin\alpha\cos\beta\pm\cos\alpha\sin\beta\]
となり、\(\sin(\alpha\pm\beta)\) の加法定理が得られました!
\(\tan\) の加法定理
最後に、\(\tan\) の加法定理を見ていきます。
こちらは、\(\cos,\sin\) の加法定理と、\(\tan\theta=\frac{\sin\theta}{\cos\theta}\) という関係から簡単に導出できます!
\[\begin{alignat*}{3}
&\tan(\alpha\pm\beta) \\
&=\frac{\sin(\alpha\pm\beta)}{\cos(\alpha\pm\beta)}\ \Bigr(\because\ \tan\theta=\frac{\sin\theta}{\cos\theta}\Bigl) \\
&=\frac{\sin\alpha\cos\beta\pm\cos\alpha\sin\beta}{\cos\alpha\cos\beta\mp\sin\alpha\sin\beta}\ {\small(\because\ \cos,\sin\ の加法定理)} \\
&=\frac{(\sin\alpha\cos\beta\pm\cos\alpha\sin\beta)\times\frac{1}{\cos\alpha\cos\beta}}{(\cos\alpha\cos\beta\mp\sin\alpha\sin\beta)\times\frac{1}{\cos\alpha\cos\beta}} \\
&=\frac{\frac{\sin\alpha}{\cos\alpha}\cdot 1\pm\frac{\sin\beta}{\cos\beta}\cdot 1}{1\mp\frac{\sin\alpha}{\cos\alpha}\cdot\frac{\sin\beta}{\cos\beta}} \\
&=\frac{\tan\alpha\pm\tan\beta}{1\mp\tan\alpha\tan\beta}\ \Bigr(\because\ \tan\theta=\frac{\sin\theta}{\cos\theta}\Bigl)
\end{alignat*}\]
となり、\(\tan(\alpha\pm\beta)\) の加法定理が得られました!
おわりに
お疲れさまでした!今回は、加法定理について解説しました。
導出の仕方が少々トリッキーで、単位円上の2点間の距離を次の2つで表し、これらが等しいという関係式を作ることで求めました。
- 単純に、距離を求める
- \(-\alpha\) だけ、原点中心に回転させて、距離を求める
確かに、大学受験という極度の緊張感の中で、初見でこの方法を思いつくかと言われると、(東京大学の受験生であったとしても、)結構厳しいものがある気がします。
ぜひ、加法定理に限らず、当たり前に利用している定理・公式も、「1度は導出を経験」しておくようにしましょう!
(私自身も、このブログ作成を通じて、1度は経験しておくということの大切さを、改めて感じました。)



コメント