【剰余の定理】
整式 \(P(x)\) が与えられたとき、\(P(x)\) を 1次式 \((\alpha x+\beta)\) で割った余りは、
\[P\Bigl(-\frac{\beta}{\alpha}\Bigr)\]
【因数定理】
整式 \(P(x)\) が与えられたとき、
\[P(x)\ が\ (\alpha x+\beta) を因数に持つ \Leftrightarrow P\Bigl(-\frac{\beta}{\alpha}\Bigr)=0\]
今回は、「剰余の定理」と「因数定理」を解説します。
これらは、内容が似ている上、同じくらいの時期に学習するため、ゴチャゴチャにして覚えられがちです。
そして、ゴチャゴチャに中途半端に覚えた結果、どんな定理かよくわからない!→数学キライ!となってしまう方がとても多い印象です。。。
これらの定理は、言っていることや、その証明はそれほど難しくない上、使いこなせれば非常に有用なツールとなります。
ぜひ、今回の解説を通じて、有用な武器を身に着けましょう!
解説
剰余の定理
剰余の定理の使い方:割り算しなくても、代入するだけで簡単に余りが求められる!
まずは、剰余の定理から見ていきます。
最初に具体例を見てみましょう。
<例>
\(P(x)={x}^{3}+3{x}^{2}-5x+6\) を \((x+1)\) で割った余り
まず、愚直に割り算をしてみると、以下のようになり、余りは \(13\) とわかります。
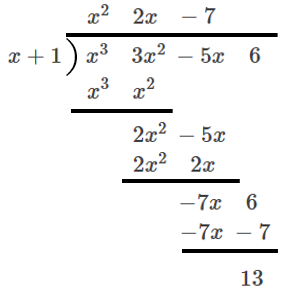
次に、剰余の定理を利用して余りを求めてみます。割る式を \(x+1=x\)\(-(-1)\) と考えて、\(P(x)\) に、\(x=-1\) を代入します。すると、
\[\begin{alignat*}{3}
P(-1)&={(-1)}^{3}+3\cdot{(-1)}^{2}-5\cdot(-1)+6 \\
&=-1+3+5+6=13
\end{alignat*}\]
となり、先ほどの割り算の結果と一致しました!
今回の例で見た3次の場合であれば、割り算をしても、それほど大変ではなかったかもしれません。
しかし、3次→4次→5次→・・・と割られる式の次数が増えていったとき、割り算がかなり大変になるのは、想像に難くないと思います。(計算量が増えると、計算ミスも発生しやすくなります)
こんなとき、剰余の定理なら、\(x\) に代入するだけで、余りが求められる、というのが、非常にうれしいポイントとなります!
剰余の定理を使えば、割り算をしなくても、\(x\) に代入するだけで、余りが求められる!
剰余の定理の証明
それでは、こちらの剰余の定理がなぜ成り立つのか、証明を見ていきましょう。
【剰余の定理】
整式 \(P(x)\) が与えられたとき、\(P(x)\) を 1次式 \((\alpha x+\beta)\) で割った余りは、
\[P\Bigl(-\frac{\beta}{\alpha}\Bigr)\]
<証明>
\(P(x)\) を 1次式 \((\alpha x+\beta)\) で割った余りは、定数(\(x\) の0次式)となります。(※)
この余りを定数 \(R\)、商を \(Q(x)\) とすると、
\[P(x)=(\alpha x+\beta)Q(x)+R\]
と書けます。
ここで、両辺に、\(x=-\frac{\beta}{\alpha}\) を代入すると、
\[\begin{alignat*}{3}
P\Bigl(-\frac{\beta}{\alpha}\Bigr)&=\Biggl\{\alpha\cdot\Bigl(-\frac{\beta}{\alpha}\Bigr)+\beta\Biggr\}Q\Bigl(-\frac{\beta}{\alpha}\Bigr)+R \\
&=0\cdot Q\Bigl(-\frac{\beta}{\alpha}\Bigr)+R=R
\end{alignat*}\]
となり、求める余り \(R\) が、\(P\Bigl(-\frac{\beta}{\alpha}\Bigr)\) となることが示されました。
(証明終了)
※ここでは、整式 \(P(x)\) を \(x\) の \(n\) 次式で割った余りは、高々 \(x\) の \((n-1)\) 次式になることを利用しています。
因数定理
因数定理の使い方:割り算しなくても、因数の目星が付けられる!
続いて、因数定理を見ていきます。
こちらも、まずは具体例を見てみましょう。
<例>
\(P(x)={x}^{4}+6{x}^{3}+5{x}^{2}-2x-10\) を因数分解する
こちらの式に、\(x=1\) を代入すると、
\[\begin{alignat*}{3}
P(x)&={1}^{4}+6\cdot{1}^{3}+5\cdot {x}^{2}-2\cdot 1-10 \\
&=1+6+5-2-10=0
\end{alignat*}\]
したがって、\(x=1\) を代入して、\(P(1)=0\) となったので、\(P(x)\) は、\((x-1)\) を因数に持つことがわかります。
実際に因数分解してみると、
\[\begin{alignat*}{3}
P(x)&={x}^{4}+6{x}^{3}+5{x}^{2}-2x-10 \\
&=(x-1)({x}^{3}+7{x}^{2}+12x+10)
\end{alignat*}\]
ここでさらに、\(P_{1}(x)={x}^{3}+7{x}^{2}+12x+10\) とおき、\(x=-5\) を代入すると、
\[\begin{alignat*}{3}
P_{1}(-5)&={-5}^{3}+7\cdot {(-5)}^{2}+12\cdot(-5)+10 \\
&=-125+175-60+10=0
\end{alignat*}\]
したがって、\(x=-5\) を代入して、\(P_{1}(-5)=0\) となったので、\(P_{1}(x)\) は、\((x+5)\) を因数に持つことがわかります。
実際に因数分解してみると、
\[\begin{alignat*}{3}
P_{1}(x)&={x}^{3}+7{x}^{2}+12x+10 \\
&=(x+5)({x}^{2}+2{x}+2)
\end{alignat*}\]
\(P(x)=(x-1)P_{1}(x)\) なので、まとめると、
\[P(x)=(x-1)(x+5)({x}^{2}+2{x}+2)\]
と因数分解することができました!
もし、因数定理を利用しない場合、実際に、\(P(x)\) を \((x\pm 1)\)、\((x\pm 2)\)、、、と順に割り算して、割り切れるかどうかを確かめていくことになります。
、、、が、割り算をするには、結構時間がかかりますよね。
こんなとき、因数定理なら、\(x\) に代入するだけで、因数かどうか判定できるため、因数の目星をつける段階で、わざわざ割り算をしなくてもいいというのが、非常にうれしいポイントとなります!
因数定理を使えば、割り算をしなくても、\(x\) に代入するだけで、因数の目星が付けられる!
因数定理の証明
それでは、こちらの因数定理がなぜ成り立つのか、証明を見ていきましょう。
【因数定理】
整式 \(P(x)\) が与えられたとき、
\[P(x)\ が\ (\alpha x+\beta) を因数に持つ \Leftrightarrow P\Bigl(-\frac{\beta}{\alpha}\Bigr)=0\]
<証明>
\(P(x)\) を 1次式 \((\alpha x+\beta)\) で割った余りは、定数(\(x\) の0次式)となります。(※)
この余りを定数 \(R\)、商を \(Q(x)\) とすると、
\[P(x)=(\alpha x+\beta)Q(x)+R\quad・・・(※)\]
と書けます。
(⇒の証明)
次の2つは、同じことを言っています。(同値)
- \(P(x)\) が \((\alpha x+\beta)\) を因数に持つ
- \(P(x)\) が \((\alpha x+\beta)\) で割り切れ、 \(R=0\) となる
したがって、⇒の証明として、\(R=0\) のときに、\(P\Bigl(-\frac{\beta}{\alpha}\Bigr)=0\) となることを証明します。
(※)の両辺に、\(x=-\frac{\beta}{\alpha}\) を代入すると、
\[\begin{alignat*}{3}
P\Bigl(-\frac{\beta}{\alpha}\Bigr)&=\Biggl\{\alpha\cdot\Bigl(-\frac{\beta}{\alpha}\Bigr)+\beta\Biggr\}Q\Bigl(-\frac{\beta}{\alpha}\Bigr)+R \\
&=0\cdot Q\Bigl(-\frac{\beta}{\alpha}\Bigr)+R=R
\end{alignat*}\]
したがって、\(R=0\) のとき、\(P\Bigl(-\frac{\beta}{\alpha}\Bigr)=0\) となることが証明できました。(⇒の証明終了)
(⇐の証明)
ここでも、これらが同値である、ということを利用します。
- \(P(x)\) が \((\alpha x+\beta)\) を因数に持つ
- \(P(x)\) が \((\alpha x+\beta)\) で割り切れ、 \(R=0\) となる
つまり、⇐の証明として、\(P\Bigl(-\frac{\beta}{\alpha}\Bigr)=0\) のときに、\(R=0\) となることを証明します。
(※)の両辺に、\(x=-\frac{\beta}{\alpha}\) を代入すると、
\[\begin{alignat*}{3}
P\Bigl(-\frac{\beta}{\alpha}\Bigr)&=\Biggl\{\alpha\cdot\Bigl(-\frac{\beta}{\alpha}\Bigr)+\beta\Biggr\}Q\Bigl(-\frac{\beta}{\alpha}\Bigr)+R \\
&=0\cdot Q\Bigl(-\frac{\beta}{\alpha}\Bigr)+R=R
\end{alignat*}\]
今、左辺 \(=P\Bigl(-\frac{\beta}{\alpha}\Bigr)=0\) なので、右辺 \(=R=0\) となり、\(P\Bigl(-\frac{\beta}{\alpha}\Bigr)=0\) のとき、\(R=0\) となることが証明できました。(⇐の証明終了)
(証明終了)
※ここでは、整式 \(P(x)\) を \(x\) の \(n\) 次式で割った余りは、高々 \(x\) の \((n-1)\) 次式になることを利用しています。
※剰余の定理で得られた、\(P\Bigl(-\frac{\beta}{\alpha}\Bigr)=R\) という関係を利用すると、因数定理が成立するのは明らか、とも言えますが、今回は解説のため、「⇒の証明」「⇐の証明」に、丁寧に分けて証明してみました。
おわりに
お疲れさまでした!今回は、「剰余の定理」と「因数定理」を見てきました。
ここまで読んでいただければ、それぞれの定理を、どういうときに使うか、ご理解いただけたのではないでしょうか。
- 剰余の定理:余りが知りたいときに、いちいち割り算しなくても、余りを計算できる!
- 因数定理:因数分解したいときに、いちいち割り算しなくても、因数の目星を付けられる!
そして、どちらもそれほど難しいことはやっていないと感じていただけたのではないかと思います。
整式の問題は、掴みどころがなく、少々とっつきづらいこともあり、共通テストなどでは、受験生みんながニガテとする部分です。逆に言えば、それだけ周りと差をつけるチャンス!とも言えます。
ぜひ、一度、「剰余の定理」「因数定理」など、正式に関する基本定理を整理して、周りと差をつけていきましょう!



コメント