等比数列（一般項・和の公式）

解説

等比数列の一般項

初項 \(a\)，公比 \(r\) の等比数列 \(\{{a}_{n}\}\) は、次の図のように表されます。

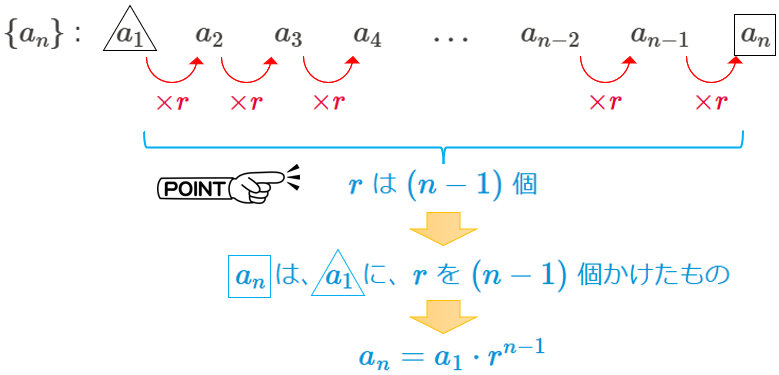
そのため、初項を \(a\) とすると、\[{a}_{n}=a\cdot r^{n-1}\]となります。

等比数列の和

初項 \(a\)，公比 \(r\) の等比数列 \(\{{a}_{n}\}\) について、初項から第 \(n\) 項までの和 \({S}_{n}\) は、次のように表すことができます。

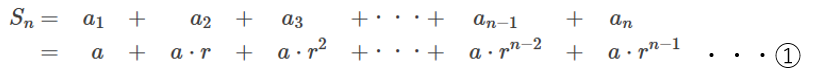
\(r=1\) の場合

\(1\) は何乗しても \(1\) なので、①は以下のように書けます。\[{S}_{n}=a+a+a+・・・+a+a\]

そして、右辺は、\({a}_{1}\) から \({a}_{n}\) の \(n\) 項の和なので、\[{S}_{n}=an\]と書けます。

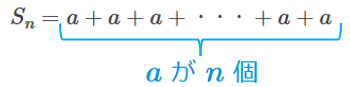
\(r\ne 1\) の場合

①の両辺に \(r\) をかけると、

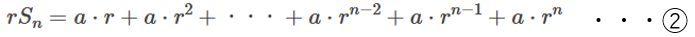
①と②を、\(r\) の乗数が等しい項が縦に並ぶようにして、両辺を引き算すると、

このように、

間の項が全て \(0\) になり、　\((1-r){S}_{n}=a-a\cdot {r}^{n}\)　　だけ残る

ことがわかります。

\(r \ne1(\Leftrightarrow\ 1-r\ne 0)\) であることに注意して、両辺を \((1-r)\) で割ると、\[{S}_{n}=\frac{a(1-{r}^{n})}{1-r}\]を得られました。（併せて、分母は \(a\) で括っています）

（補足）等比数列の和の公式に現れる、分母の乗数について

試験などで緊張していると、\[{S}_{n}=\frac{a(1-{r}^{n})}{1-r}\]の分母の \(r\) が、\(n\) 乗だよな？いや、\(n-1\) 乗だったかも・・・？　と不安になることがあると思います。（少なくとも、私は何度か経験した記憶があります。。。）

その場合は、公式を導出した、この筆算を思い出しましょう。

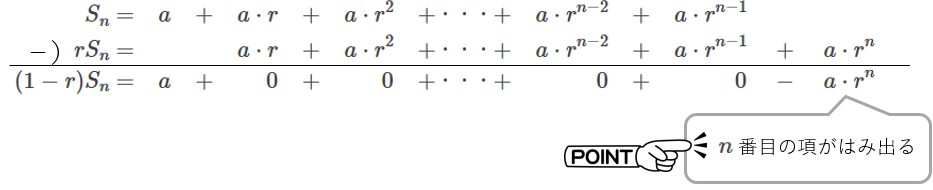
そうすると、一番右側の \(n\) 番目の項がはみ出して、そのまま分母に来る　ことがわかると思います。ぜひお試しください！

おわりに

今回は、等比数列の一般項と、和の公式を解説しました。

等比数列の公式は、公式の丸暗記ではなく、どのように導出するかを理解すること　がとても重要です。
導出方法を理解できれば、万一、試験中に忘れてしまっても、自分で簡単に導出できますし、そもそも公式も忘れづらくなります。
特に、補足で取り上げた「分母の \(r\) が \(n\) 乗か、\(n-1\) 乗か」という問題は、試験中などの非常に緊張感が高まる現場では、多くの受験生が経験するものです。

公式の導出方法について不安な方は、何度も読み返して、ぜひ数列を得点源にしましょう！